Question

A man of mass $M$ having a bag of mass $m$ slips from the roof of a tall building of height $H$ and starts falling vertically. When at a height of $h$ from the ground, he notices that the ground below him is pretty hard, but there is a pond at a horizontal distance $x$ from the line of fall. In order to save himself he throws the bag horizontally (with respect to himself) in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in the water. If the man just succeeds to avoid the hard ground, where will the bag land?

Answer 1

Hint
The momentum of the man and the bag will be conserved in the horizontal direction. So using the conservation laws, we can find the velocity needed for the bag. We can substitute the value of the velocity of the man with ${x \mathord{\left/ {\vphantom {x t}} \right.} t}$ where we get the time from the equations of motion of the man falling vertically. Now since the center of mass of the man and the bag doesn’t change in the horizontal direction so using that we can find the distance travelled by the bag.
Formula Used: In this solution we will be using the following formula,
$S = ut + \dfrac{1}{2}g{t^2}$
where $S$ is the distance travelled,
$u$ is he initial velocity
$t$ is the time taken and $g$ is the acceleration due to gravity
and $V = \dfrac{S}{t}$ where $V$ is the velocity

Complete step by step answer
To solve this problem, we need to first draw the diagram of the situation.

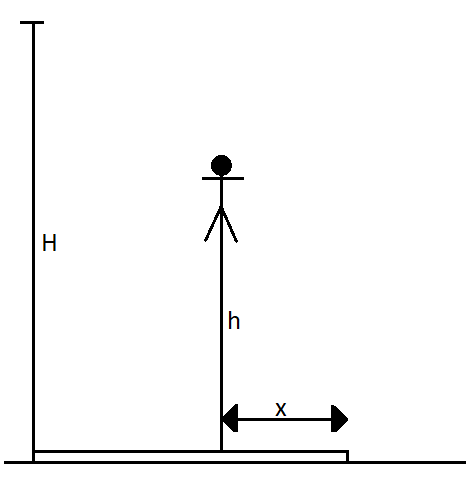
Now at the height $h$ , the man throws the bag to the left in order to fall into the pond on his right. Since there is no net force acting on the man in the horizontal direction, so the momentum of the man will be conserved in that direction. Therefore from the law of conservation of momentum we have,
$0 = mv + MV$ where $v$ and $V$ are the velocity of bag and man respectively.
Therefore we get,
$mv = - MV$
The negative sign is because the horizontal velocity of the bag is in the opposite direction to that of the man. If we take only the magnitudes, then we can write,
$mv = MV$
From here we can write the velocity of the bag as,
$v = \dfrac{M}{m}V$
The $V$ is the velocity of the man in the horizontal direction. This is given by the horizontal distance $x$ divided by the time $t$ taken by the man to fall the height $h$ .
That is $V = \dfrac{x}{t}$
Let the time taken by the man to fall the whole height $H$ be $T$ . So this time $T$ is given from the equation of motion as,
$H = 0 + \dfrac{1}{2}g{T^2}$
From here we can take all variables to the other side except $T$ and write,
${T^2} = \dfrac{{2H}}{g}$
Taking square root on both sides,
$T = \sqrt {\dfrac{{2H}}{g}}$
Now let the time taken by the man to fall the height $\left( {H - h} \right)$ be $T'$ . So this time $T'$ is given from the equation of motion as,
$H - h = 0 + \dfrac{1}{2}g{T'^2}$
From here we can take all variables to the other side except $T'$ and write,
${T'^2} = \dfrac{{2\left( {H - h} \right)}}{g}$
Taking square root on both sides,
$T' = \sqrt {\dfrac{{2\left( {H - h} \right)}}{g}}$
So the time taken for the man to fall the height $h$ is
$t = T - T'$
Substituting the values we get
$t = \sqrt {\dfrac{{2H}}{g}} - \sqrt {\dfrac{{2\left( {H - h} \right)}}{g}}$
We take $\sqrt {\dfrac{2}{g}}$ common we get,
$t = \sqrt {\dfrac{2}{g}} \left( {\sqrt H - \sqrt {H - h} } \right)$
Substituting the value of $t$ in the equation of the horizontal velocity of the man we get,
$V = \dfrac{x}{{\sqrt {\dfrac{2}{g}} \left( {\sqrt H - \sqrt {H - h} } \right)}}$
So therefore the velocity $v$ imparted to the bag in the horizontal direction is
$v = \dfrac{M}{m}\dfrac{x}{{\sqrt {\dfrac{2}{g}} \left( {\sqrt H - \sqrt {H - h} } \right)}}$
Now since there is no net force in the horizontal direction, the center of mass of the man and the bag will remain the same.
Therefore, we can write,
$0 = \dfrac{{Mx + mx'}}{{M + m}}$
Where $x'$ is the horizontal distance travelled by the bag.
So therefore, from the equation we can write
$Mx + mx' = 0$
Taking $Mx$ to the RHS we get,
$mx' = - Mx$
Dividing both sides by $m$ we get
$x' = - \dfrac{{Mx}}{m}$
The negative sign shows that the direction the bag falls is opposite to the man.

Note
In this problem we have used the law of conservation of momentum, where it states that in the absence of net unbalanced force on a body, the sum of the momentum will always remain constant. Since the man was falling vertically, we have taken the momentum to be zero in the first case.