Question

A man of mass 70 kg stands on a weighing scale in a lift which is moving.
A. Upwards with uniform speed of $10\text{ m}{{\text{s}}^{-1}}$
B. Downwards with uniform acceleration of $5\text{ m}{{\text{s}}^{-2}}$
C. Upwards with uniform acceleration of $5\text{ m}{{\text{s}}^{-2}}$ what would be the reading on the scale in each case
D. What would be the reading if the lift mechanism failed and it hurtled down freely under gravity

Answer 1

We have been provided with a lift, inside which weight mechanism placed over which man is standing. In part (a) pseudo force is zero therefore net force experienced by weight is mg only, put the value and you will get readings. In part (b) lift is moving in downwards direction; therefore pseudo force acts upwards direction. Hence the resultant force experience by weight machine is mg-ma. In part (c) the resultant force experience by weight machine is mg + ma. This way you will get all readings for all cases. In the last part (d) mechanism of the lift failed and it is falling freely under gravity i.e. acceleration of the lift is g and hence acceleration of man is also g. put values in resultant force i.e. m (g-a) and get the readings which are given by the weight machine.

Complete step by step answer:
We have been provided with lift in which the weighing machine is placed. Consider now a man of 70 kg weight standing on a weighing machine. Now we need to calculate the weight of a man measured by a weighing machine in different cases.
A. In the first case, lift is moving in an upwards direction with a uniform speed of $10\text{ m}{{\text{s}}^{-1}}$and we need to calculate the reading which is measured by the weighing machine.

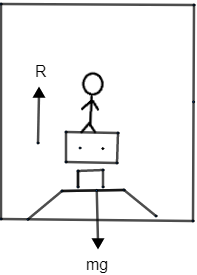
Since, lift is moving upwards hence we will go with frame of lift As you can see in the figure an mg force acts on weighing machine and opposite to that, an reaction force acts by an weighing machine therefore expression can written as,
$R=mg......\left( 1 \right)$
Here, mg force is balanced by reaction force. R is the reaction force. We know that value of m is 70kg and value of acceleration due to gravity is 10, put all values in equation (a) we get,
$R=70\times 10=700N$
Hence, 700N would be the reading on the scale in this case.
B. Now, in (b) case, lift is moving in downwards direction with a uniform acceleration of $5\text{ m}{{\text{s}}^{-2}}$
And we need to calculate reading on the scale of the weighing machine.

Now the lift is acceleration in downwards direction i.e. lift is in non-inertial frame. If we consider lift as frame then pseudo force will act on man in upwards direction which is ma and to balance this force mg is acting in downwards direction hence, the net force experienced by the weight machine is mg-ma.
$\begin{aligned} & R=mg-ma \\\ & R=m(g-a) \\\ & R=70(10-5) \\\ & R=70\times 5 \\\ & R=350N \\\ \end{aligned}$
Hence, the 350N would be the reading on the scale of the weight machine when lift accelerated in downwards direction.
C. In part (c), lift is moving in upwards direction, therefore pseudo force will act in downwards direction. So, and the net force experience by weight is mg + ma
$\begin{aligned} & R=m(10+5) \\\ & =70\times 15 \\\ & R=1050N \\\ \end{aligned}$
Hence, 1050N could be the reading on the scale of a weight machine when lift moves in an upwards direction with uniform acceleration.
D. In this case, if the lift mechanism failed then the whole lift and the things inside the lift fell freely under the gravity. I.e. if acceleration of the whole set up is g (since it is falling freely under gravity) then acceleration of man will also be g i.e. a=g here lift is moving downwards therefore resultant force or net force experienced by the weight machine is mg-ma.
$\begin{aligned} & R=m(g-a) \\\ & R=m(a-a)(\therefore a=g) \\\ & R=m(0) \\\ & R=0 \\\ \end{aligned}$
Hence zero would be the reading if the mechanism fails.

Note: Here value of g is taken as $10\text{ m}{{\text{s}}^{-1}}$ to make calculation easy generally value of $g=9.8m/{{s}^{2}}$. In part (a) lift is moving in upwards direction therefore pseudo force acts in downwards direction. But speed is uniform I.e. The acceleration of lift is zero, hence pseudo force also is zero. In part (b) lift is moving in downward direction therefore net force experienced by the weight machine is m (g-a) if lift is moving in upwards direction then net force experienced by the machine is m (g + a). In this question we have neglected resistance or forces acted by air. If resistance of air is included then this question will no longer be the case of a free body.