Solveeit Logo
Login

Question

Question: A man of mass \(60kg\) climbs up a \(20m\) long staircase to the top of a building \(10m\) high. Wha...

A man of mass 60kg60kg climbs up a 20m20m long staircase to the top of a building 10m10m high. What is the work done by him? (Take g=10ms−2g = 10m{s^{ - 2}} ).
A. 12kJ12kJ
B. 6kJ6kJ
C. 3kJ3kJ
D. 18kJ18kJ

Explanation

Solution

In order to solve this question you have to know the concept of gravitational potential energy and what is the formula for gravitational potential energy? Also, remember that the work done against gravity is equal to the change in gravitational potential energy of the body.

Formula used:
Gravitational potential energy is given by,

P.E=mghP.E = mgh

Where mm is the mass of the body
gg is the acceleration due to gravity
hh is the height at which the body is

Complete step by step solution:

Here, in the question, the mass of the mass is given by,

m=60kgm = 60kg

And it is given that he climbs at the top of the building of height which is given by,

h=10mh = 10m

And also the acceleration due to gravity is given in the question as,

g=10ms−2g = 10m{s^{ - 2}}

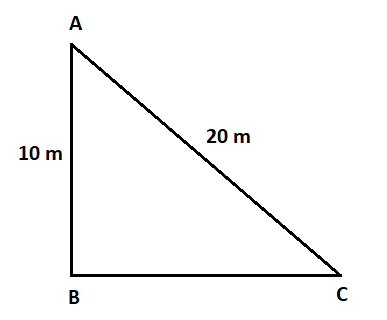
Here it is given that the man is at point A
We have to find the work done by the man
So, as we know that the work done is equal to the change in potential energy
Hence, at point C the potential energy is given by,

(P.E)C=mgh=0{(P.E)_C} = mgh = 0 (as the value of height is zero at this point)

Now, the potential energy at point A is given by,

(P.E)A=mgh{(P.E)_A} = mgh

At this point, h=10mh = 10m, m=60kgm = 60kg and g=10ms−2g = 10m{s^{ - 2}}
On putting all the values we have in the above equation, we get

(P.E)A=60×10×10=6000J{(P.E)_A} = 60 \times 10 \times 10 = 6000J

Now, the work done by the man is given by,
Work done == change in potential energy

⇒W=(P.E)A−(P.E)C \Rightarrow W = {(P.E)_A} - {(P.E)_C}

On putting values from equation (i) and (ii), we have

⇒W=6000J=6kJ \Rightarrow W = 6000J = 6kJ

Therefore, the correct option is (B).

Note: Gravitational potential energy is defined as the energy of an object which is due to its position relative to some other object. For example when you stand on the ground floor of a building then you have less potential energy than when you are standing at the top of that building because the force of gravity is acting on you and doing work in the process. The work done by a certain force is actually the product of the force times the displacement along the line of action of the force. So, if force is acting and the displacement happens to occur at an angle then we take the component of force that is along the displacement.