Question

A man of height $h$is walking away from a street lamp with a constant speed $v.$ The height of the street lamp is $3h.$ The rate at which length of the man’s shadow is increasing when he is at a distance $10h$ from the base of the street lamp is

Answer 1

Hint : $\dfrac{{dy}}{{dx}}$ represents the rate of change of $y$ with respect to $x.$ Assume the length of the man’s shadow to be $y$ and the distance from the street lamp at which he is standing to be $x.$ Then find the rate of change of $y$ with respect to $x.$

Complete step-by-step answer :
Let the horizontal distance of man from the street lamp be $x$
Let the length of the shadow of the man be $y$

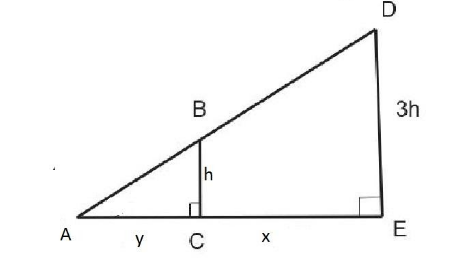
From the above figure we can say that
In $\Delta ACB$and $\Delta AED$
$\angle A = \angle A$(Common)
$\angle C = \angle E = {90^0}$ (Right angle)
$\angle B = \angle D$ (If two angles of two triangles are equal then the third angle must be equal as well)
Therefore, by AAA criteria of similarity of two triangles, we get
$\Delta ACB \approx \Delta AED$
Since, the ratio of the corresponding sides of similar triangles is equal, we can write
$\dfrac{{DE}}{{BC}} = \dfrac{{AE}}{{AC}}$
$\Rightarrow \dfrac{{3h}}{h} = \dfrac{{x + y}}{y}$
Cancelling the common terms, we get
$\Rightarrow \dfrac{{x + y}}{y} = 3$
By cross multiplying, we get
$x + y = 3y$
Re-arranging, we get
$\Rightarrow 3y - y = x$
$\Rightarrow 2y = x$
Different both the sides with respect to $x.$
$\Rightarrow \dfrac{{2dy}}{{dx}} = 1$
$\Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{1}{2}$

Note : You need to find derivatives to find the rate of change. But to differentiate, you need to find a relation between the required variables. For that, you need to use some other properties like, similarity, trigonometric equations etc. So, just knowing differentiation is not enough.