Question

A man of height $180{\text{ cm}}$ is moving away from the lamp post at the rate of $1.2{\text{m per second}}$. If the height of the lamp post is $4.5{\text{m}}$
Find the rate at which
(1) His shadow is lengthening
(2) The tip of his shadow is moving.

Answer 1

In order to solve this question we will try to make the sketch of the situation and then see the lengths which we need to find and then we can apply the differentiation method to get the speed as we know that the differentiation of the distance with respect to time gives us the speed.
For example if we get $y = 3x$ then differentiating both the sides with respect to time will give us the relation between their speeds.

Complete step-by-step answer:
Here we are given that height of the man is $180cm = 1.8m$
Now we also know that he is moving away from the lamp post at the rate of $1.2{\text{m per second}}$ and height of the lamp is also given as $4.5m$
Now let us visualise the situation and sketch the figure for it as given

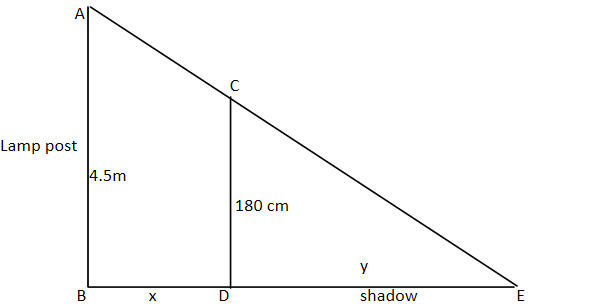
Here we can say
Length $AB =$ lamp post$= 4.5m$
$CD = {\text{man}}$ $= 180cm = 1.8m$
$DE = {\text{shadow}}$
And distance of the tip $E$ at the shadow from the pole is $BE$ $= x + y$
Now In
$\Delta ABE{\text{ and }}\Delta CDE \\\ \angle E = \angle E{\text{ common angle in both}} \\\ \angle ABE = \angle CDE = 90 \\\ \angle BAE = \angle DCE{\text{ (corresponding angles)}} \\\$
So we can say $\Delta ABE \sim \Delta CDE$

So we can write
$\dfrac{{AB}}{{CD}} = \dfrac{{BE}}{{DE}}$
$\Rightarrow$ $\dfrac{{4.5}}{{1.8}} = \dfrac{{x + y}}{y}$
$\Rightarrow 4.5y = 1.8x + 1.8y \\\ \Rightarrow y = \dfrac{2}{3}x \\\$
Now differentiating both the sides with respect to Time which is $t$ we get
$\Rightarrow$ $\dfrac{{dy}}{{dt}} = \dfrac{2}{3}\dfrac{{dx}}{{dt}}$
We know that according to the question we are given
$\Rightarrow$ $\dfrac{{dx}}{{dt}} = 1.2m/\sec$
Hence we can say that
$\Rightarrow$ $\dfrac{{dy}}{{dt}} = \dfrac{2}{3}\dfrac{{dx}}{{dt}}$ $= \dfrac{2}{3}(1.2) = 0.8m/\sec$
As the length of the shadow is $y$ hence we can say the shadow is lengthening with the speed of $0.8m/\sec$
Also we know that $BE = x + y$
So $\dfrac{{d(BE)}}{{dt}} = \dfrac{{dx}}{{dt}} + \dfrac{{dy}}{{dt}}$
$= 1.2 + 0.8 = 2m/\sec$
Hence the rate at which the tip of the shadow is moving away is $2m/\sec$

Note: In this type of question we need to visualise the situation clearly and then proceed by first making the clear figure and then see the situation. Here we must be clear with the grammatical errors while reading the question and proceed with the proper calculations.