Question

A man of 170cm wants to see his complete image in the mirror (while standing) His eyes are at a height of 160cm from the ground.
A. Minimum length of the mirror = 80cm
B. Minimum length of the mirror = 85cm
C. Bottom of the mirror should be at a height of 80cm
D. Bottom of the mirror should be at a height of 85cm

Answer 1

This question can be solved in two parts. Firstly, you could recall the expression for the minimum length of the mirror that has to be used for viewing the full length of a man. Now you could use the same expression for finding the height at which the bottom of the mirror should be kept. But for the second part the height to be substituted would be the height at which the eyes are present.

Formula used:
${{L}_{\min }}=\dfrac{h}{2}$

Complete solution:
In the question, we are given a man of 170cm height who wants to see his complete image in a mirror while standing. His eyes are said to be at a height of 160cm from the ground. Using this information, we are asked to find which among the given conditions is true.

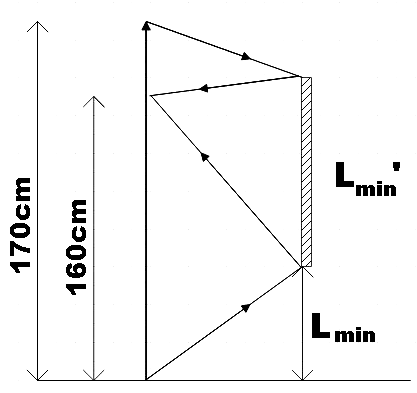
Let us recall that the minimum length of the plane mirror in order to see the full height of a person’s body is given by,
${{L}_{\min }}'=\dfrac{h}{2}$
Where, h is the height of the man.
So, we are already given the value of the height of the man as,
$h=170cm$
So, the minimum length of the mirror would be,
${{L}_{\min }}=\dfrac{170}{2}$
$\therefore {{L}_{\min }}=85cm$
Similarly, the minimum height at which the bottom of the mirror should be is got by using the same formula, that is,
${{L}_{\min }}=\dfrac{H}{2}$
But the H here is the height at which man’s eyes are present from the bottom. So,
${{L}_{\min }}=\dfrac{160}{2}$
$\therefore {{L}_{\min }}=80cm$
Therefore, we found that the bottom of the mirror should be at a height of 80cm or more in order to satisfy the given conditions.
Therefore, we found that,
Minimum length of the mirror = 85cm
Bottom of the mirror should be at a height of 80cm

Hence, we found that option B and option C to be the correct statements.

Note:
An alternative method that can be used to solve this question is by making a ray diagram of the given condition and then considering similar triangles. Doing so, you will end up in the same answers as that in the above method. The method that we used in the above solution saves time and thus can be considered comparatively better to the alternative method though the alternative method gives better conceptual clarity.