Question
Question: A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed...
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30∘ to 45∘ in 12 minutes. Find the time taken by the car now to reach the tower.
Solution
Hint : We can use the concept of trigonometric ratio. Drawing the diagram and finding which ratio will help to solve the question is the key.
Formula Required:
tanθ=adjacent sideopposite side
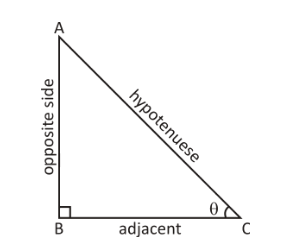
tan30∘=31 tan45∘=1
3=1.732
Distance is the product of speed and time.
Complete step-by-step answer :
Given: man observes a car from the top of a tower
Car is moving at a uniform speed.
Angle of depression of the car changes from 30∘ to 45∘ in 12 minutes.
We need to find time taken by the car from second position to reach the bottom of the tower.
Let’s consider the below figure,
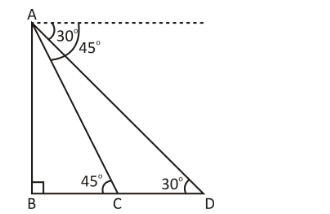
Where,
AB is the height of the tower
Initial position of the car is at D
Next position of the car is at C
30∘ and 45∘ are the angle of depressions of a car from the top of the tower.
Let CD=d1
CB=d2
Time taken from D to C is t1
According to the question, t1=12 minutes.
Time taken from C to B is t2
From Triangle ABC,
tan45∘ = adjacent side to 45∘opposite side to 45∘ ⇒tan45∘ = BCAB
We know that tan45∘=1
⇒1=BCAB ⇒AB=BC
⇒AB=BC=d2 …………..Equation(1)
From Triangle ABD,
tan30∘ = adjacent side to 30∘opposite side to 30∘ ⇒tan30∘=BDAB ⇒tan30∘=BC + CDAB
We know that tan30∘=31
⇒31=BC + CDAB
⇒BC + CD=3AB …………..Equation(2)
Substituting Equation(1) in Equation(2) we get,
⇒d2+d1=3d2 ( CD = d1 and CB = d2 ) ……….Equation(3)
Distance is the product of speed and time.
⇒d1 = s1×t1 ⇒d1 = s×12
Similarly,
⇒d2=s2×t2 ⇒d2=s×t2
Since the car travels with uniform speed s1=s2=s
Now substituting the values of d1 and d2 in equation (3) we get,
Approximating 3=1.732 we get,
t2=16.39 Minutes.
Therefore time taken by the car from second position to reach the bottom of the tower is 16.39 minutes.
So, the correct answer is “ 16.39 minutes”.
Note : In the questions involving heights and distances concept the diagram leads to forming right triangles, In that case the questions tests us about the trigonometric ratios. We need to have an idea about the definition of trigonometric ratios and the values of angle of the same. As per the data given in the question we need to figure out which ratio will help us to find the answer.
