Question

A man moves towards a plane mirror with a velocity $v$ in a direction making an angle $\theta$ with the normal to the mirror. The magnitude of velocity of image relative to man normal to the mirror will be:
A. $2v$
B.$\dfrac{{2v}}{{\sin \theta }}$
C. $2v\sin \theta$
D. $2v\cos \theta$

Answer 1

Determine the velocity of the man moving towards the plane mirror and the velocity of the image of the man moving towards the man. Then determine the velocity of image relative to man normal to the mirror.

Complete step by step answer:
The man is moving towards a plane mirror with a velocity $v$ making an angle $\theta$ with the normal.

The image also moves towards the man with the same velocity $v$.

The diagram representing the velocities of the man and his image is as follows:]

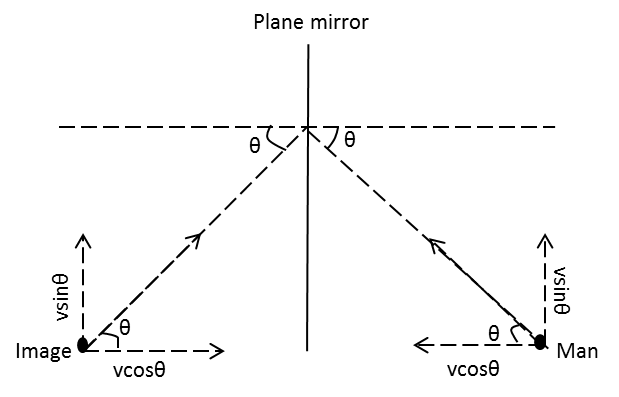
In the above figure, $- v\cos \theta$ and $v\sin \theta$ are the components of velocity of the man perpendicular and parallel to the normal respectively. Also, $v\cos \theta$ and $v\sin \theta$ are the components of velocity of the image perpendicular and parallel to the normal respectively.

Hence, the velocity ${v_m}$ of the man perpendicular to the normal is $- v\cos \theta$ and velocity ${v_i}$ of the image perpendicular to the normal is $v\cos \theta$.
${v_m} = - v\cos \theta$
${v_i} = - v\cos \theta$

Calculate the velocity of the image relative to man normal to the mirror.

The velocity ${v_{im}}$ of the image relative to the man normal to the mirror is the subtraction of the velocity ${v_i}$ of the image perpendicular to the normal and velocity ${v_m}$ of the man perpendicular to the normal.
${v_{im}} = {v_i} - {v_m}$

Substitute $v\cos \theta$ for ${v_i}$ and $- v\cos \theta$ for ${v_m}$ in the above equation.
${v_{im}} = \left( {v\cos \theta } \right) - \left( { - v\cos \theta } \right)$
$\Rightarrow {v_{im}} = 2v\cos \theta$

Therefore, the velocity and the magnitude of the image relative to man normal to the mirror is $2v\cos \theta$.

Hence, the correct option is D.

Note: One may also consider the man is moving from left towards the plane mirror instead of from right. Then the required velocity of the image will be $- 2v\cos \theta$. But the magnitude of the velocity still remains the same as $2v\cos \theta$.