Question

A man moves on a horizontal road towards east at a speed of 1 km/hr and the rain appears to him vertically at a speed of 2 km/hr. the actual speed of the rain (in km/hr) is
$\text{A}\text{. }1$
$\text{B}\text{. }\sqrt{2}$
$\text{C}\text{. }\sqrt{3}$
$\text{D}\text{. }\sqrt{5}$

Answer 1

Use the formula for the relative velocity of body B with respect to body A. With that, find an expression for the actual speed of body B. Then substitute the given values and find the actual speed of the rain.
Formula used:
$\overrightarrow{{{v}_{BA}}}=\overrightarrow{{{v}_{B}}}-\overrightarrow{{{v}_{A}}}$

Complete answer:
It is given that a man is moving on a horizontal road towards with a speed of 1 km/hr and it is raining. When the man is moving with this speed, he sees that the rain is appearing to fall vertically at a speed of 2 km/hr.
The motion of the rain seen by the man is called as the relative motion of the rain with respect to the man. The man sees the rain coming down vertically, but the actual speed and direction (i.e. velocity) of the rain will be different.
When two bodies A and B are in motion with velocities $\overrightarrow{{{v}_{A}}}$ and $\overrightarrow{{{v}_{B}}}$, then the relative velocity of the body B with respect to body A is given as $\overrightarrow{{{v}_{BA}}}=\overrightarrow{{{v}_{B}}}-\overrightarrow{{{v}_{A}}}$
$\Rightarrow \overrightarrow{{{v}_{B}}}=\overrightarrow{{{v}_{BA}}}+\overrightarrow{{{v}_{A}}}$.
Here, the actual velocity of the man and the relative velocity of the rain with respect to the man are perpendicular.

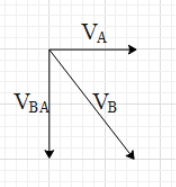
Therefore, the actual speed of rain is ${{v}_{B}}=\sqrt{v_{BA}^{2}+v_{A}^{2}}$ ….. (i).
In this case, ${{v}_{BA}}=2km{{h}^{-1}}$ (i.e. speed of the man) and ${{v}_{A}}=1km{{h}^{-1}}$ (i.e. speed of the rain with respect to the man).
Substitute the velocities in equation (i).
${{v}_{B}}=\sqrt{{{2}^{2}}+{{1}^{2}}}=\sqrt{5}km{{h}^{-1}}$.
This means that the actual speed of the rain is $\sqrt{5}km{{h}^{-1}}$.

Hence, the correct option is D.

Note:
We have only found the actual speed of the rain in this question. The actual direction of rain will also be different. We can find it by drawing the vector diagram of the velocities.
Note that the formula for the relative velocity of B with respect to A only works with the velocities of the bodies. We cannot apply the same formula for finding the speeds. Meaning, we cannot directly substitute the speed of the bodies in that formula.
Relative motion is not only about speed but the direction of relative motion also matters.