Question

A man moves in an open field Such that after moving $10\,{\text{m}}$ on a straight line, he makes a sharp turn of $60^\circ$ to his left. The total displacement just at the start of 8th turn is equal to:
A. $12\,{\text{m}}$
B. $15\,{\text{m}}$
C. $17.32\,{\text{m}}$
D. $14.14\,{\text{m}}$

Answer 1

Use the formula for the resultant of the two vectors. This formula will give the relation between the magnitudes of the two vectors and the angle made by the two vectors. The man will be travelling along the sides of a hexagon according to the information given. Determine the angle between the two vectors when the man takes his 7th and 8th turn and determine the displacement of the man.

Formula used:
The magnitude of the resultant of the two vectors $\vec A$ and $\vec B$ is given by
$R = \sqrt {{A^2} + {B^2} + 2AB\cos \theta }$ …… (1)
Here, $A$ is the magnitude of the vector $\vec A$, $B$ is the magnitude of the vector $\vec B$ and $\theta$ is the angle between the vectors $\vec A$ and $\vec B$.

Complete step by step solution:
We have given that a man is moving in an open field such that it moves $10\,{\text{m}}$ and then makes a turn of $60^\circ$ to his left.
For each turn the man is making an angle of $60^\circ$ to his left. If the man continues his motion in the same way, we can conclude that the man is moving along the edges of a hexagon as the angle made by two sides of a hexagon with the horizontal is $60^\circ$.
Hence, after taking 6 turns, the man reaches at the initial point of his journey. Thus, the displacement of the man after 6 turns is zero as he reaches the original point of his journey.
The man travels along the next two adjacent sides of the hexagon to complete 8 turns.
The path of the man for the 7th and 8th turn is as shown in the following figure:

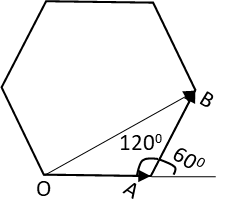
The point O is the initial position of the man. The 7th turn of the man is shown by the vector $\vec A$ and the 8th turn is shown by vector $\vec B$.
The angle between the two sides of a hexagon is always $120^\circ$.
The sum of the angles made on a single straight line is $180^\circ$.
Hence, the angle between the vectors $\vec A$ and $\vec B$ is $180^\circ - 120^\circ = 60^\circ$.
The magnitude of the each vectors $\vec A$ and $\vec B$ is $10\,{\text{m}}$ as the distance travelled during each turn is $10\,{\text{m}}$.
The resultant of the vectors $\vec A$ and $\vec B$ is the vector $OB$ which gives the total displacement at 8th turn.
We can determine the magnitude $R$ of the vector OB using equation (1).
Substitute $10\,{\text{m}}$ for $A$, $10\,{\text{m}}$ for $B$ and $60^\circ$ for $\theta$ in equation (1).
$R = \sqrt {{{\left( {10\,{\text{m}}} \right)}^2} + {{\left( {10\,{\text{m}}} \right)}^2} + 2\left( {10\,{\text{m}}} \right)\left( {10\,{\text{m}}} \right)\cos 60^\circ }$
$\Rightarrow R = \sqrt {100 + 100 + 200\cos 60^\circ }$
$\Rightarrow R = \sqrt {200 + 200\cos 60^\circ }$
$\Rightarrow R = \sqrt {200 + 200\left( {\dfrac{1}{2}} \right)}$
$\Rightarrow R = \sqrt {300}$
$\Rightarrow R = 17.32\,{\text{m}}$
Therefore, the displacement of the man at the start of the 8th turn is $17.32\,{\text{m}}$.

So, the correct answer is “Option C”.

Note:
One can also take the angle between the two vectors as $120^\circ$. But this is the angle made by the two vectors with the negative direction of the X-axis. Hence, the angle between the vectors becomes $- 120^\circ$. Since the cosine of a positive angle and cosine of the negative of the same angle are equal. Hence, we will get the same final answer.