Question
Question: A man is travelling on the road along \(AB\), find out the length road for which the image will be v...
A man is travelling on the road along AB, find out the length road for which the image will be visible to him:
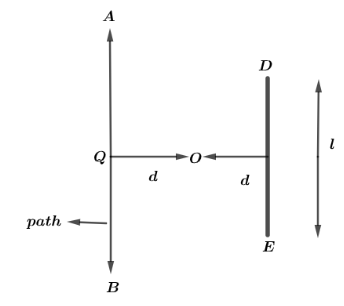
A. l
B. 3l
C. 1.5l
D. 2l
Solution
We can solve this question by tracing the light ray’s path and form an image behind the plane mirror DE and hence will find the length of AB and will use simple geometry of congruent triangles. Image due to a plane mirror is always formed behind the mirror.
Complete step by step answer:
Let us first draw the ray diagram of the given question. Draw a light ray from O to D and O to E. Let M be the mirror and let triangle AQR and DMR.
Both are right angled triangles and angle <R is common in them which shows,
Both triangles are congruent and hence, using the ratio of sides we get,
DMAQ=MRQR→(i)
Now, the side AQ is half of the total side 2x which implies that
AQ=x
And side DM is half of the total side l which implies that,
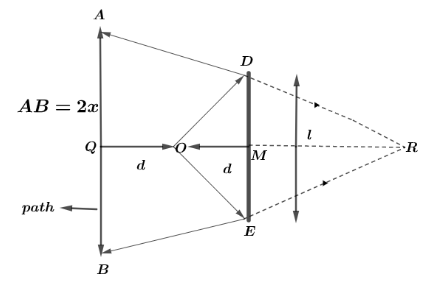
DM=2l
From diagram we also know,
QR=3d As distance MR=d because object O lies at a distance of d from the mirror M
So, MR=d .
Now, we will put these values in the equation (i). We get,
l2x=3
⇒x=23l
But, we need to find the length of
AB=2x
∴AB=3l
So the distance of the road must be of length 3l in order to form a full image through the mirror.
Hence, the correct option is B.
Note: Remember, the condition for the congruence of two right angle triangle is such that, both must be right angles triangle and an angle other than 90∘ must be equal, than both triangles will be congruent and every congruent triangles are similar hence their ratio of side will be equal.
