Question

A man is standing on the deck of a ship which is 10 m above the water level. He observes the angle of elevation at the top of hill as ${{60}^{\circ }}$ and angle of base of hill as ${{30}^{\circ }}$ . Find the height of the hill from the base.

Answer 1

Hint: Here, we have to draw the figure with the given data. Let $CD$be the height of the hill. i.e.
$CD\text{ }=\text{ }CE\text{ }+\text{ }ED$. Consider $\vartriangle ABC$ , calculate $AE=BC$ by evaluating $\tan {{30}^{\circ }}$ and then consider $\vartriangle AED$ , calculate $ED$ by evaluating $\tan {{30}^{\circ }}$ . We have:
$\tan \theta =\dfrac{opposite\text{ }side}{adjacent\text{ }side}$

Complete step-by-step answer:
First we have to draw the figure with the given data.

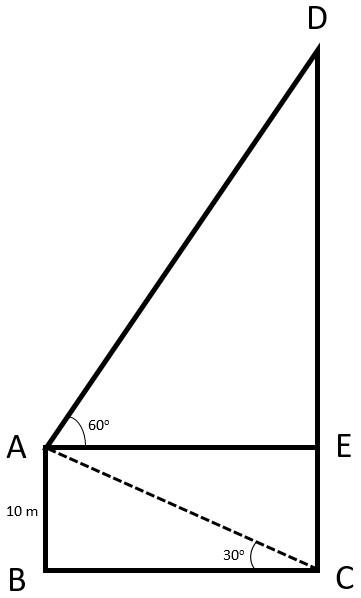
Here, given that a man standing at the deck of the ship is 10 m above the sea level. Also given that the angle of elevation at the top of the hill is ${{60}^{\circ }}$ .The angle of depression at the base of hill is ${{30}^{\circ }}$ .
Now, we have to calculate the height of the hill from the base.
We have $AB=10m$
The angle of elevation is , $\angle EAD={{60}^{\circ }}$
The angle of depression is $\angle BCA={{30}^{\circ }}$
Let $CD$ be the height of the hill. From the figure we can say that:
$CD=CE+ED$
First we have to find $ED$. For that consider the $\vartriangle ABC$ ,
We know that,
$\tan \theta =\dfrac{opposite\text{ }side}{adjacent\text{ }side}$
Therefore, we will get:
$\tan {{60}^{\circ }}=\dfrac{ED}{AE}$
We have $\tan {{60}^{\circ }}=\sqrt{3}$ . Hence we will get :
$\sqrt{3}=\dfrac{ED}{AE}$
From the figure we can say that $AE=BC$ . Hence we will obtain:
$\sqrt{3}=\dfrac{ED}{BC}\text{ }.....\text{ (1)}$
Now let us find $BC$ for that consider $\vartriangle ABC$ .
$\tan {{30}^{\circ }}=\dfrac{AB}{BC}$
We know that $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$ , $AB=10m$. Therefore we will obtain:
$\dfrac{1}{\sqrt{3}}=\dfrac{10}{BC}$
Now, by cross multiplication we get:
$BC=10\sqrt{3}$
Next, substitute the value $BC=10\sqrt{3}$ in equation (1) we get:
$\sqrt{3}=\dfrac{ED}{10\sqrt{3}}\text{ }$
Now, by cross multiplication we get:
$\begin{aligned} & ED=10\sqrt{3}\times \sqrt{3} \\\ & ED=10\times 3 \\\ & ED=30 \\\ \end{aligned}$
Next, we have to find $CD$ where $CD=CE+ED$
We know that $AB=CE=10m$ and $ED=30$ . Hence we get:
$\begin{aligned} & CD=10+30 \\\ & CD=40 \\\ \end{aligned}$
Therefore, we can say that the height of the hill from the base is $40m$.

Note: Here, instead of $\vartriangle ABC$ you can also consider $\vartriangle AEC$ since $\angle BCA=\angle EAC={{30}^{\circ }}$ , i.e. they are alternate interior angles.