Solveeit Logo
Login

Question

Question: A man is standing on an incline which makes angle \(\theta \) horizontal and rain is falling vertica...

A man is standing on an incline which makes angle θ\theta horizontal and rain is falling vertically with respect to man. Now man starts walking along the incline

A. if man walks up the incline, rain may appear to come horizontal
B. if man walks down the incline, rain may appear to come horizontally
C. no matter whether man walks up or down, rain can never appear to come horizontal
D. if man walks (up or down) along incline rain may appear to come along the inclined

Explanation

Solution

To solve this question we will use the concepts of vector addition which depends on the angle between the two vectors. Take the direction of the velocity of rain and the velocity of the man given in the conditions and find out which options are correct with the help of vector addition.

Complete answer:

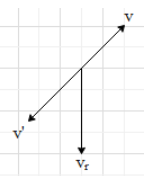
Let, vr{{v}_{r}} is the velocity of the rain falling vertically downward with respect to the man in rest.
Let, the man walks up the incline with a velocity v. So, the relative velocity of the man to the rain will be in the opposite direction. Let this velocity is v′=v{v}'=v
If we take the resultant of the velocities vr{{v}_{r}} and v′{v}', the resultant velocity of the rain will be in a direction between the vr{{v}_{r}} and v′{v}'. So, the rain will not appear to come horizontally when the man walks up the incline.

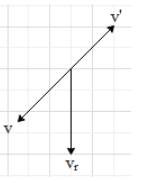
Let, vr{{v}_{r}} is the velocity of the rain falling vertically downward with respect to the man in rest.
Let, the man walks down the incline with a velocity v. So, the relative velocity of the man to the rain will be in the opposite direction. Let this velocity is v′=v{v}'=v
If we take the resultant of the velocities vr{{v}_{r}} and v′{v}', the resultant velocity of the rain will be in a direction between the vr{{v}_{r}} and v′{v}'. Now, if the component of v′{v}'in the vertical direction can cancel the velocity of the rain, then we can get a velocity in the horizontal direction. So, the rain may appear horizontal if the man walks down the incline.
The third option is wrong, because when the man walks down the incline, rain may come vertically.
Now, in both the cases, the resultant velocity of the rain will be in a direction between vr{{v}_{r}} and v′{v}'. It cannot be in the direction of v′{v}'because, for this to happen the velocity of rain should be zero. So, the fourth option is also wrong.

The correct option is (B).

Note:
If we have two vectors A⃗\vec{A} and B⃗\vec{B} in a plane making an angle θ\theta with each other, then the resultant vector can be found from vector addition of the two vectors mathematically as,
R⃗=A⃗+B⃗\vec{R}=\vec{A}+\vec{B}
And the direction of the resultant vector can be simply found out by using trigonometric functions.