Question

A man is running towards the west with a speed of 5$$$$km/hr.It appears to him that rain is falling vertically downwards. When he increases his speed to 8$$$$km/hr, it appears to him that rain is falling ${30^ \circ }$ with the vertical. Find the magnitude of velocity of rain with respect to ground and its direction?

Answer 1

As, required calculated quantities have both magnitude and direction, then we will use the vector concept to solve the question.
We will denote the velocity of man and rain separately using different vector variables.

Formula Used:
We will use the following formulas:
$\tan \theta = \dfrac{\text{Perpendicular}}{\text{Base}}$
$\sin \theta = \dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$
And, $\cos \theta = \dfrac{\text{Base}}{\text{Hypotenuse}}$
As, the man’s speed and rain has a two way direction plot, velocity of man and rain will have two different notations of $\hat i$ and$\hat j$.
Pythagoras theorem, ${(Perpendicular)^2} + {(Base)^2} = {\text{Hypotenuse}^2}$.

Complete step by step answer:
Initially, the man was walking towards the west and no rain fell. But, then rain started falling vertically, so the direction of rain was changing as the man’s speed increased. So due to increase in speed there one more vector rises between rain falling and man’s speed.
Let us consider,
The velocity of the man is {V_{Man}} = 5$$$$km/hr
And, the vector representation of velocity is${\vec V_{Man}}$ and the vector representation of the velocity of rain and man is ${\vec V_{R - M}}$ and, the vector representation of rain is${V_R}$.
We can state the following equations:
{\vec V_{Main}} = {V_{Man}} \times ( - \hat i) = 5 \times ( - \hat i) = - 5\hat i$$$$km/hr.
And, {V_{R - M}} = v \times ( - \hat j) = - v\hat j$$$$km/hr.

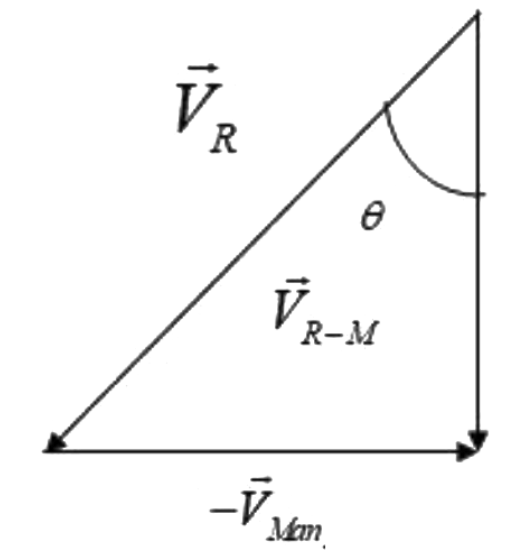
With respect to the diagram we can write the following equation:
$\sin \theta = \dfrac{{{V_{Man}}}}{{{V_R}}}$
Or, ${V_R}\sin \theta = {V_{Man}} = 5$.
But, the velocity of the man increased later to 8$$$$km/hr.
So, the new velocity became ${\vec V_{Man\\_new}} = 8 \times ( - \hat i) = - 8\hat i$.
Now, the angle of vector of velocity made by rain and man is${30^ \circ }$.
Let us draw the following image:

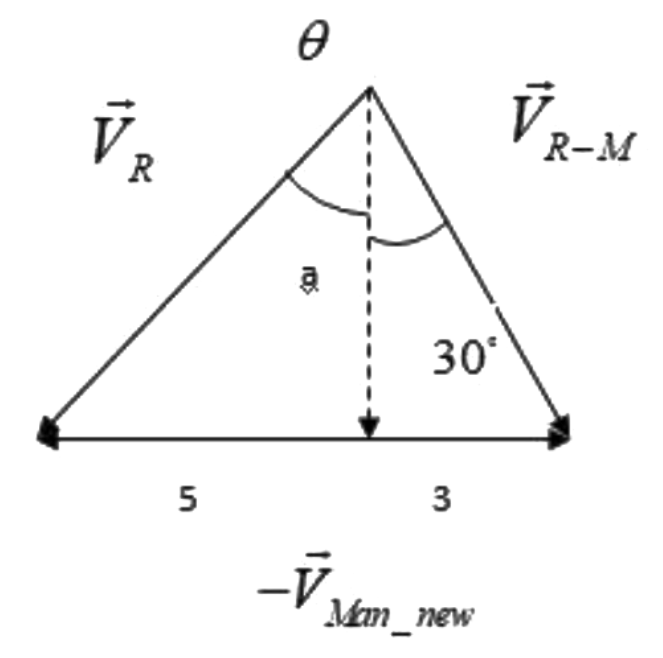
So, we can say that,
$\tan {30^ \circ } = \dfrac{3}{a}$
And, $\tan \theta = \dfrac{5}{a}$.
By simplifying, we get:
$a = \dfrac{3}{{\tan {{30}^ \circ }}} = \dfrac{3}{{\dfrac{1}{{\sqrt 3 }}}} = 3\sqrt 3$, as value of $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$.
And, $\tan \theta = \dfrac{5}{a} = \dfrac{5}{{3\sqrt 3 }}$.
We can re-draw the above image as:

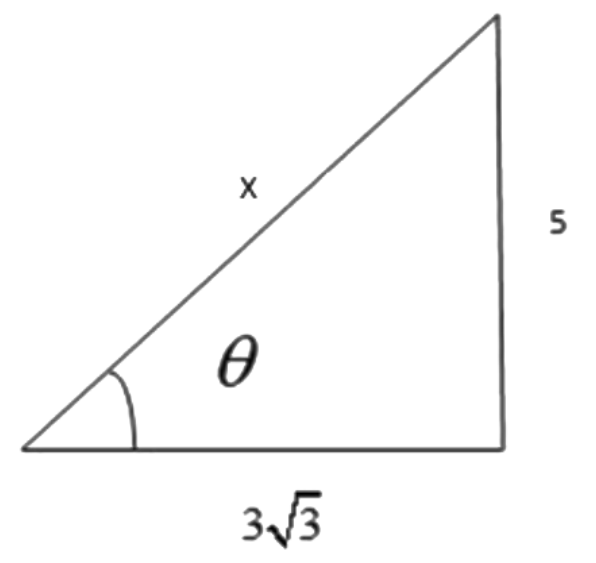
By using Pythagoras theorem,
${5^2} + {(3\sqrt 3 )^2} = {x^2}$
Or, ${x^2} = 25 + 27$
Or, ${x^2} = 52$
Or, $x = \sqrt {52}$
From the above image we can say that:
$\sin \theta = \dfrac{5}{{\sqrt {52} }}$.
But, we found that${V_R} = \dfrac{5}{{\sin \theta }}$.
So, ${V_R} = \dfrac{5}{{\dfrac{5}{{\sqrt {52} }}}}$
Or, ${V_R} = \sqrt {52}$.
Or, ${V_R} = 7.21$
$\therefore$ The magnitude of the velocity will be 7.21$$$$km/hr.

Note: Vector is a quantity which has both magnitude and direction but has no position. In contrast to vectors, if any quantity that has a magnitude but not a direction is called scalars.