Question

A man is going in a topless car with a velocity of $10.8\,kmh{r^{ - 1}}$. It is raining vertically downwards. He has to hold the umbrella at an angle of ${53^ \circ }$ to the vertical to protect himself from rain. The actual speed of the rain is $\left( {\cos {{53}^ \circ } = \dfrac{3}{5}} \right)$
(A) $2.25\,m{s^{ - 1}}$
(B) $3.75\,m{s^{ - 1}}$
(C) $0.75\,m{s^{ - 1}}$
(D) $2.75\,m{s^{ - 1}}$

Answer 1

This problem can be solved by using trigonometric functions and using the concept of relative velocity. By using the given information and the angle of the umbrella, the triangle should be made and then by using the trigonometric function the velocity or speed of the rain can be determined.

Complete step by step answer:
Given that,
The velocity of car, ${V_c} = 10.8\,kmh{r^{ - 1}}$
The velocity of car, ${V_c} = 3\,m{s^{ - 1}}$
The angle of umbrella with respect to the vertical, $\theta = {53^ \circ }$

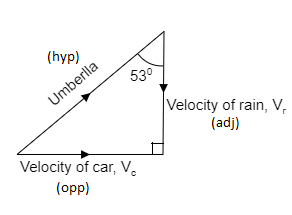
Now, from the diagram, by taking the $\tan \theta$, the velocity of the rain can be determined.
In trigonometry, $\tan \theta$ is equal to the opposite side divided by adjacent sides.
$\tan \theta = \dfrac{{{V_c}}}{{{V_r}}}\,................\left( 1 \right)$
Where, $\theta$ is the angle of the umbrella, ${V_c}$ is the velocity of the car, ${V_r}$ is the velocity of the rain.
Substituting the velocity of car and the angle of umbrella in the above equation (1), then,
$\tan {53^ \circ } = \dfrac{3}{{{V_r}}}$
From trigonometry, the value of $\tan {53^ \circ }$ is $1.327$, substitute this value in the above equation, then the above equation is written as,
$1.327 = \dfrac{3}{{{V_r}}}$
By keeping the velocity of rain in one side and the other terms in another side, then the above equation is written as,
${V_r} = \dfrac{3}{{1.327}}$
By dividing the above equation in RHS, then the above equation is written as,
${V_r} = 2.26\,m{s^{ - 1}}$
Thus, the velocity of the rain is approximately equal to $2.25\,m{s^{ - 1}}$.
Hence, the option (A) is the correct answer.

Note: While taking the angle of the umbrella, we have to be more careful because the angle of the umbrella is vertical. And the unit of the velocity of the car $kmh{r^{ - 1}}$ is converted into $m{s^{ - 1}}$, because the unit of the speed of rain is given in $m{s^{ - 1}}$.