Question

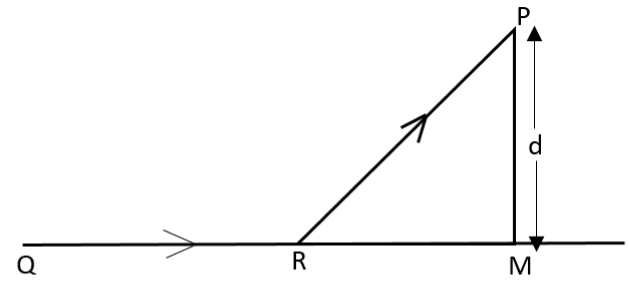
A man in a car at location Q on a straight highway is moving with speed v. He decides to reach a point P in a field at a distance d from the highway (Point M) as shown in figure. Speed of the car in the field is half to that on the highway. What should be the distance RM, so that the time taken to reach P is the minimum?

Answer 1

We will use derivatives to calculate minimum hence, and basic formula of distance and speed to solve the question. Find out the expression for the time taken by the car to reach at point P and differentiate the time equation with respect to distance RM. The time will be the minimum when the first derivative of the time is zero.

Formula used:
$t = \dfrac{s}{v}$
Where, t is the time, s is the distance and v is the velocity.

Complete step by step answer:
Let the distance from $R$to $M$ be $x$
i.e. $RM = x$
It is given that the car is moving at the speed $v$.i.e. speed of car from $Q$ to $R$ is $v$.
The distance between $P$ and $M$ is $d$
.i.e. $PM = d$
Speed of cars in the field is half to that on the highway.
. i.e. the speed of car from $R$ to $P$ is $\dfrac{v}{2}$
Now, we know that,
${\text{Time}} = \dfrac{{{\text{Distance}}}}{{{\text{Velocity}}}}$
Therefore, the time taken to travel from $Q$to $R$ $= {t_1} = \dfrac{{QR}}{V}$
$\Rightarrow {t_1} = \dfrac{{QM - x}}{V}$ . . . . . (1)
And time taken to travel from $R$to $P$ in the field$= {t_2} = \dfrac{{RP}}{{\dfrac{V}{2}}}$ . . . . . (2)
By Pythagoras theorem,
$R{P^2} = R{M^2} + P{M^2}$
$\Rightarrow R{P^2} = {x^2} + {d^2}$
$\Rightarrow RP = \sqrt {{x^2} + {d^2}}$

By substituting this value in (2) we get
${t_2} = \dfrac{{\sqrt {{x^2} + {d^2}} }}{{\dfrac{v}{2}}}$
$\Rightarrow {t_2} = \dfrac{{2\sqrt {{x^2} + {d^2}} }}{v}$ . . . . . (3)
The total time to travel from $Q$to $P$be $t$. Then,
$t = {t_1} + {t_2}$
$\Rightarrow t = \dfrac{{QM - x}}{v} + \dfrac{{2\sqrt {{x^2} + {d^2}} }}{v}$
For the time taken to be minimum,
$\dfrac{{dt}}{{dx}} = 0$.
First calculate $\dfrac{{dt}}{{dx}}$ by differentiating
Equation (1) with respect to $x$
$\Rightarrow \dfrac{{dt}}{{dx}} = \dfrac{1}{v}( - 1) + \dfrac{2}{v} \times \dfrac{1}{{2\sqrt {{x^2} + {d^2}} }}\dfrac{1}{{dx}}({x^2})$
$\left( {\because \dfrac{d}{{dx}}{x^n} = n{x^{n - 1}}} \right)$
And $\dfrac{d}{{dx}}f\left( {g\left( x \right)} \right) = \dfrac{{df}}{{dx}} \times \dfrac{{dg\left( x \right)}}{{dx}}$
$\dfrac{d}{{dx}}f(g(x)) = {f^1}g(x).\dfrac{d}{{dx}}g(x)$
$\Rightarrow \dfrac{{dt}}{{dx}} = - \dfrac{1}{v} + \dfrac{{2x}}{{v\sqrt {{x^2} + {d^2}} }}$. . . . . (5)
$\because \dfrac{{dt}}{{dx}} = 0$
$\Rightarrow - \dfrac{1}{v} + \dfrac{{2x}}{{v\sqrt {{x^2} + {d^2}} }} = 0$

Multiplying both the sides by $v$
We get,
$- 1 + \dfrac{{2x}}{{\sqrt {{x^2} + {d^{^2}}} }} = 0$
$\Rightarrow \dfrac{{2x}}{{\sqrt {{x^2} + {d^2}} }} = 1$
By cross multiplication, we get
$\Rightarrow 2x = \sqrt {{x^2} + {d^2}}$
Squaring both the sides, we get
$\Rightarrow 4{x^2} = {x^2} + {d^2}$
$\Rightarrow 3{x^2} = {d^2}$
$\Rightarrow {x^2} = \dfrac{{{d^2}}}{3}$
$\Rightarrow x = \pm \dfrac{d}{{\sqrt 3 }}$
But distance cannot be negative, therefore,
$\therefore x = \dfrac{d}{{\sqrt 3 }}$

Note: In the given question, we are not given the quantities of distance or time and we have calculated the distance in terms of the total vertical distance as, $x = \dfrac{d}{{\sqrt 3 }}$. Students can also differentiate the equation (5) to determine whether the time is the minimum or not. You would directly make it as an option without calculating $\dfrac{{{d^2}t}}{{d{x^2}}}$.