Question

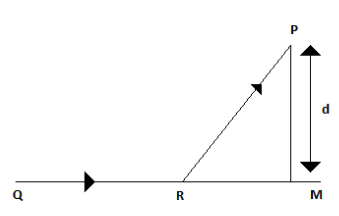
A man in a car at a location $Q$ on a straight highway is moving with speed $v$. He decides to reach a point $P$ in a field at a distance d from the highway (point $M$ ) as shown in the figure. The speed of the car in the field is half that on the highway. What should be the distance$RM$ , so that the time taken to reach $P$ is minimum?

$\left( A \right)\dfrac{d}{{\sqrt 3 }}$
$\left( B \right)\dfrac{d}{2}$
$\left( C \right)\dfrac{d}{{\sqrt 2 }}$
$(D)$ $d$

Answer 1

By calculating the time ${t_1}$ and $\;{t_2}$, We will calculate the total time. By derivation of the time with respect to $x$ we can find the minimum time taken to reach $P$.

Complete step by step answer:
From point $M$ at a distance, $x$ the car turns off the highway. Then, $RM = x$
And if the speed of the car in the field is $v$ , then the time is taken by the car to cover the distance $QR = QM - x$
On the highway, ${t_1}$ can be given by
${t_1} = \dfrac{{QM - x}}{{2v}}$
Time taken by the car to travel the distance $RP$ can be given by,
${t_2} = \dfrac{{\sqrt {{d^2} + {x^2}} }}{v}$
The total time elapsed to move from Q to P
$t = {t_1} + {t_2}$
$\Rightarrow t = \dfrac{{QM - x}}{{2v}} + \dfrac{{\sqrt {{d^2} + {x^2}} }}{v}$
If $t$ is minimum,
$\Rightarrow \dfrac{{dt}}{{dx}} = 0$
$\Rightarrow \dfrac{1}{v}\left[ { - \dfrac{1}{2} + \dfrac{x}{{\sqrt {{d^2} + {x^2}} }}} \right] = 0$
$\Rightarrow x = \dfrac{d}{{\sqrt {4 - 1} }} = \dfrac{d}{{\sqrt 3 }}$

Hence the right answer is in option $\left( A \right) \Rightarrow \dfrac{d}{{\sqrt 3 }}$.

Additional information:
${\text{Speed = }}\dfrac{{{\text{distance}}}}{{{\text{time}}}}$ : This formula describes distance traveled divided by the time taken to cover the distance.
Speed is Inversely proportional to Time and also directly Proportional to Distance.
Hence, ${{Distance = Speed \times Time}}$, and ${{Time = \;}}\dfrac{{{\text{distance}}}}{{{\text{speed}}}}\;$, as the speed increases the time taken will decrease and vice versa.

Note: Distance, speed, and Time can be expressed in different units:
Time: seconds$\left( s \right)$ , minutes$\left( {min} \right)$ , hours $\left( {hr} \right)$
Distance: meters$\left( m \right)$ , kilometers$\left( {km} \right)$ , miles, feet
Speed: $m/s$ , $km/hr$
So if Distance = $\left( {km} \right)$ and Time = $\left( {hr} \right)$, then
${\text{Speed = }}\dfrac{{{\text{Distance}}}}{{{\text{time}}}}{\text{ = }}\dfrac{{{\text{km}}}}{{{\text{hr}}}}$