Question
Question: A man has fallen into a ditch of width \(d\) and two of his friends are slowly pulling him out using...
A man has fallen into a ditch of width d and two of his friends are slowly pulling him out using a light rope and two fixed pulleys as shown in the figure. Show that the force (assumed equal for both the friends) exerted by each friend on the rope increases as the man moves up. Find the force when the man is at a depth h.
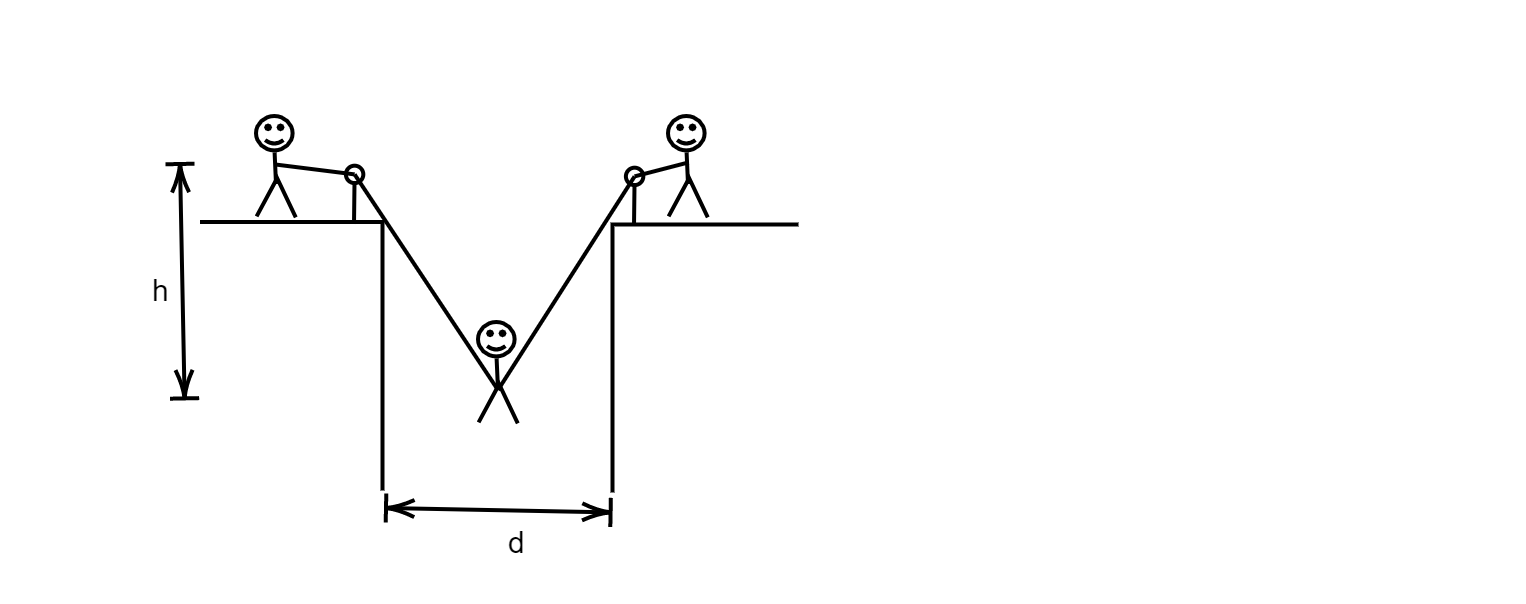
Solution
To solve these types of questions, our first step should be to make a detailed free body diagram so that we can figure out how the forces are acting on the system. Next step would be to form equations of forces and then solve them to get the required results.
Complete answer:
Let us first draw the free body diagram for better understanding and assume that the rope makes an angle θ with the vertical.
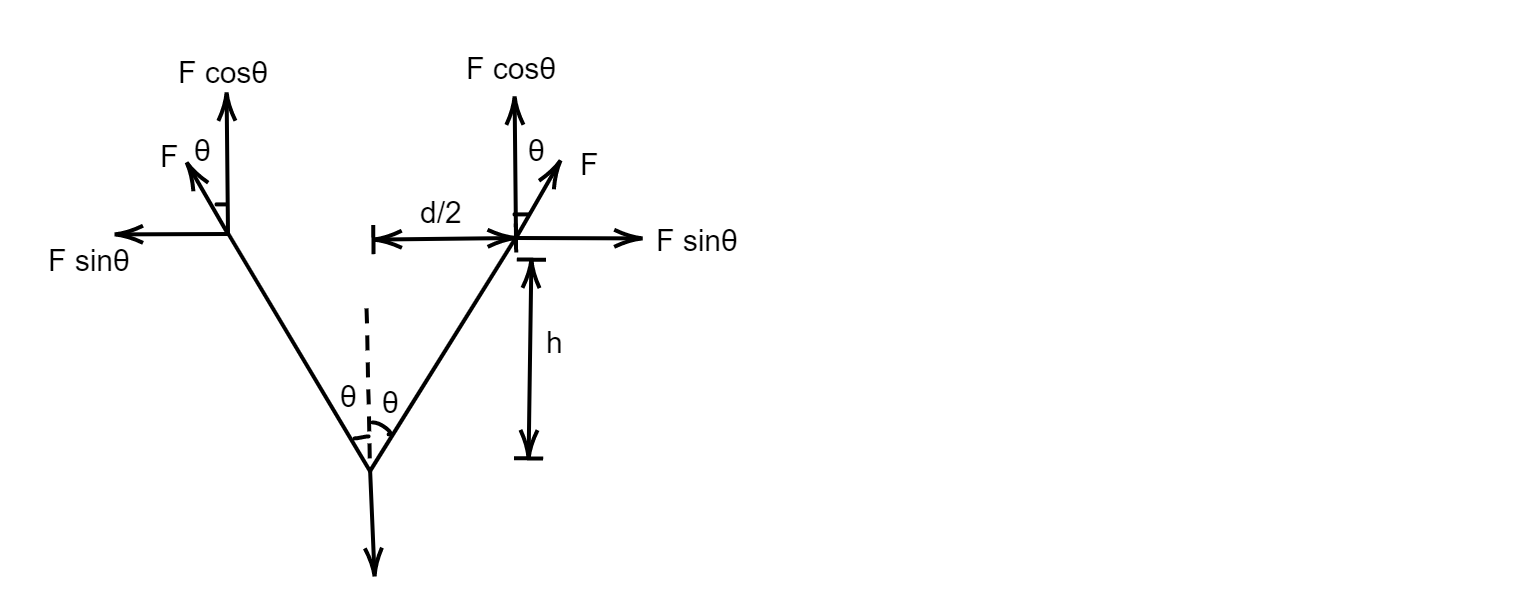
On observing the free body diagram, we can conclude that:
Fcosθ+Fcosθ=mg⇒2Fcosθ=mg⇒F=2cosθmg
As the man’s friends pull him up, the angle that the rope makes with the vertical will increase and thus cosθ will decrease.
We know that cosθ is the length of the base of a right-angle triangle divided by the length of the hypotenuse, hence in this case we will consider the depth of the ditch as the base of the triangle and the length of the rope as the length of the hypotenuse, and hence we will get the following value:
cosθ=(2d)+h2h
Substituting this value in equation of force, we get:
