Question

A man generates a symmetrical pulse in a string by moving his hand up and down. At $t = 0$ , the point in his hand moves downwards from mean position. The pulse travels with speed $3\,m{s^{ - 1}}$ on the string and his hand passes $6$ times in each second from the mean position. Then the point on the string at a distance $3\,m$ with reach its upper extreme first time at $t =$
A. $1.25$
B. $1\,s$
C. $\dfrac{{13}}{{12}}s$
D. $\dfrac{{23}}{{24}}s$

Answer 1

a man will generate a symmetrical pulse in a string by moving his hand up and down. To calculate the time at which the point on the string at a distance $3\,m$ will reach its upper extreme, we will first calculate the wavelength of the pulse. The formula for calculating the wavelength of the pulse is given below.

Formula used:
The formula for calculating the wavelength is given by
$V = f\lambda$
Here, $V$ is the speed of the pulse, $f$ is the frequency and $\lambda$ is the wavelength of the pulse.

Complete step by step answer:
Consider a man that will generate a symmetrical pulse in a string by moving his hand up and down. If the hand will pass $6$ times from the mean position in one second, then the string will create a $3$ wavelength or $3$ cycle in one second. This means that the frequency of the wave is $3Hz$ .Also, the speed of the pulse, $v = \,3\,m{s^{ - 1}}$.And the frequency of the pulse, $3Hz$. The wave showing the pulse is given below

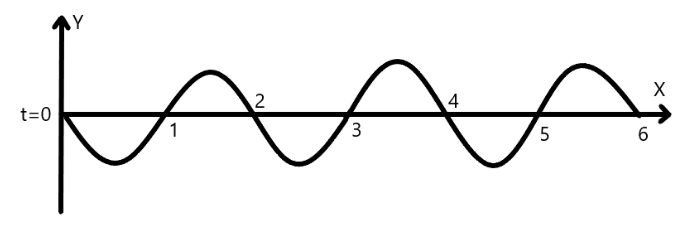
Now, to calculate the wavelength of the pulse, we will use the following formula
$V = f\lambda$
$\Rightarrow \,\lambda = \dfrac{V}{f}$
$\Rightarrow \,\lambda = \dfrac{{3\,m{s^{ - 1}}}}{{3\,Hz}}$
$\Rightarrow \,\lambda = 1m$
From this value, we can say that if the wavelength of the pulse is $\lambda = 1m$ then the point having $3\,m$ distance will be located at $6th$ position.Therefore, to reach the upper extreme, the pulse has to travel a $\dfrac{{3\lambda }}{4}$ distance.

Now, as we know, time taken by the pulse to travel a distance $3\lambda \, = \,1\,\sec$.
Also, the time taken by the pulse to travel a distance $\lambda \, = \,\dfrac{1}{3}\,\sec$.
Therefore, the time taken by the pulse to travel a distance,
$\dfrac{{3\lambda }}{4}\, = \,\dfrac{1}{3} \times \dfrac{3}{4}$
$\Rightarrow \,\dfrac{1}{4}\,\sec$
$\therefore \,0.25\,\sec$
Therefore, the time taken by the pulse to reach its upper stream is $0.25\,\sec$.

Hence, option A is the correct option.

Note: The pulse shape at any time $t$ will be the same when it is repeated. Also, there will be three crests and three troughs formed by the pulse as the pulse will be three cycles per second. As it is forming three cycles, therefore, the frequency will be in relation to the cycle.