Solveeit Logo
Login

Question

Question: A man fires a bullet of mass \(200gm\) at a speed of \(5m{{s}^{-1}}\). The gun is of one kilogram ma...

A man fires a bullet of mass 200gm200gm at a speed of 5ms−15m{{s}^{-1}}. The gun is of one kilogram mass. At what velocity, the gun rebounds back?
A.1ms−1 B.0.01ms−1 A.0.1ms−1 A.10ms−1 \begin{aligned} & A.1m{{s}^{-1}} \\\ & B.0.01m{{s}^{-1}} \\\ & A.0.1m{{s}^{-1}} \\\ & A.10m{{s}^{-1}} \\\ \end{aligned}

Explanation

Solution

This question has to be solved by considering the laws of conservation of the linear momentum. Momentum is defined as the product of mass and the velocity of the bullet. The momentum at the time of incident time will be equal to the momentum at the time of rebounding. These all may help you to solve this question.

Complete answer:

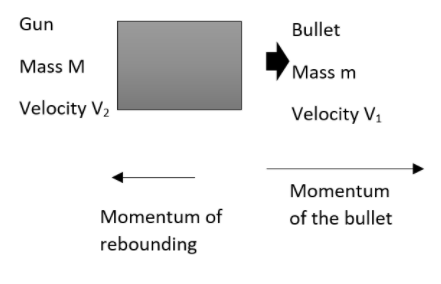
First of all let us mention what all are given in the question. The mass of the object or the bullet which is getting fired from the gun is given as,
m=200gm=200g
This bullet has been travelling with a speed of V1{{V}_{1}}.
V1=5ms−1{{V}_{1}}=5m{{s}^{-1}}
The bullet loaded gun is having a mass given as,
M=1kgM=1kg
Now we have to find the velocity with which the gun rebounds back. Therefore we can write that,
Let the velocity with which the gun rebounds back be V2{{V}_{2}}.
Therefore according to the law of conservation of linear momentum, the total momentum of the system of objects will be constant unless an external force is acting over it. Therefore in this we can say that the momentum of the bullet travelling will be equal to the momentum with which the gun rebounds back. That is we can write that,
mV1=−MV2m{{V}_{1}}=-M{{V}_{2}}
Now we can substitute the values in it,
That is we can write that,
200×5=−1000×V2200\times 5=-1000\times {{V}_{2}}
Therefore the velocity of the gun will be,
V2=−1000200×5=−1ms−1{{V}_{2}}=\dfrac{-1000}{200\times 5}=-1m{{s}^{-1}}
Here the negative sign is due to the direction difference of the two velocities. Here we have to consider only the magnitude of the velocity.
That is,
V2=1ms−1{{V}_{2}}=1m{{s}^{-1}}

Therefore the correct answer is obtained. It is given as option A.

Note:
Isaac Newton discovered the laws of linear momentum through Newton's equation of motion. It is based on the first law of motion known as law of inertia. This conservation has applications in launching rockets.