Question

A man crosses a ${\text{320 m}}$ wide river perpendicular to the current in ${\text{4}}$ minutes. If in still water he can swim with a speed $\dfrac{5}{3}$ times that of the current, then the speed of the current, in ${\text{m/min}}$ is
A. $30$
B. $40$
C. $50$
D. $60$

Answer 1

In this question, we are given the resultant velocity and velocity of the swimmer is $\dfrac{5}{3}$ times speed of the current. This question can be solved using vectors. As the resultant velocity is perpendicular, the velocity of the swimmer must be in the negative direction. Resolve the velocity of the swimmer into its component. Components along the river must be equal to the speed of current and components perpendicular to the river must be equal to resultant velocity. Solve the equations and find out the speed of the current.

Complete step by step answer:
We are given,
Width of river $= 320{\text{ m}}$
Time taken by the swimmer to cross the river ${\text{ = 4}}$ minutes
Resultant velocity of the swimmer is ${{\text{V}}_{{\text{sw}}}} = \dfrac{{320}}{4}{\text{ m/min = 80 m/min}}$
Let the velocity of the swimmer in still water be ${{\text{V}}_{\text{s}}}$
Let the speed of current be ${{\text{V}}_{\text{w}}}$
Given, ${{\text{V}}_{\text{s}}} = \dfrac{5}{3}{{\text{V}}_{\text{w}}}$
To solve this question, draw the vector diagram
Since the resultant velocity is perpendicular to the direction of speed of current swimmer must swim in the negative direction.
Let the swimmer make an angle $\theta$ with the horizontal

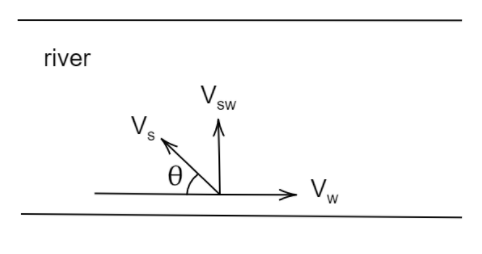
Resolve the velocity of swimmer into its components
Since the resultant velocity is in the perpendicular direction, the horizontal component of velocity of swimmer ${{\text{V}}_{\text{s}}}\cos \theta$ must cancel out ${{\text{V}}_{\text{w}}}$
Thus, ${{\text{V}}_{\text{s}}}\cos \theta = {{\text{V}}_{\text{w}}}$
But we are given, ${{\text{V}}_{\text{s}}} = \dfrac{5}{3}{{\text{V}}_{\text{w}}}$
$\Rightarrow \dfrac{5}{3}{{\text{V}}_{\text{w}}}\cos \theta = {{\text{V}}_{\text{w}}}$
Cancelling ${{\text{V}}_{\text{w}}}$ from both the sides we get,
$\Rightarrow \cos \theta = \dfrac{3}{5}$
Therefore, $\sin \theta = \dfrac{4}{5}$
The resultant velocity of the swimmer must be equal to the vertical component of swimmer velocity
${{\text{V}}_{{\text{sw}}}} = {{\text{V}}_{\text{s}}}\sin \theta$
Substituting the values we get,
$\dfrac{4}{5}{{\text{V}}_{\text{s}}} = 80$
$\Rightarrow {{\text{V}}_{\text{s}}} = 100{\text{ m/min}}$
Thus, velocity of swimmer in still water is $100{\text{ m/min}}$
We can find out the speed of current using ${{\text{V}}_{\text{s}}} = \dfrac{5}{3}{{\text{V}}_{\text{w}}}$
Substituting the values we get,
${{\text{V}}_{\text{w}}} = 60{\text{ m/min}}$
Thus, speed of the current is $60{\text{ m/min}}$
Thus, option D. is the correct option.

Note: In this type of question, always draw the vector diagram to solve the question easily and try to resolve them into components and equate. Find whether the swimmer is going upstream or downstream and the angle it is making with the horizontal using the resultant velocity.