Question

A man can swim with a speed of $4km{h^{ - 1}}$ in still water. He crosses a river $1km$ wide that follows steadily at $3km{h^{ - 1}}$. If he makes his strokes normal to the river current, how far down the river does he go when he reaches the other bank?
A) $500m$
B) $600m$
C) $750m$
D) $850m$

Answer 1

The time the swimmer spends swimming in the river is responsible for two things: he moves from one bank of the river to the other and also moves in the direction of the river due to the flow of the river. Therefore, if one calculates the time he spends crossing the river, that time can be used in calculating the distance moved in the direction of the river flow.

Complete step by step solution:
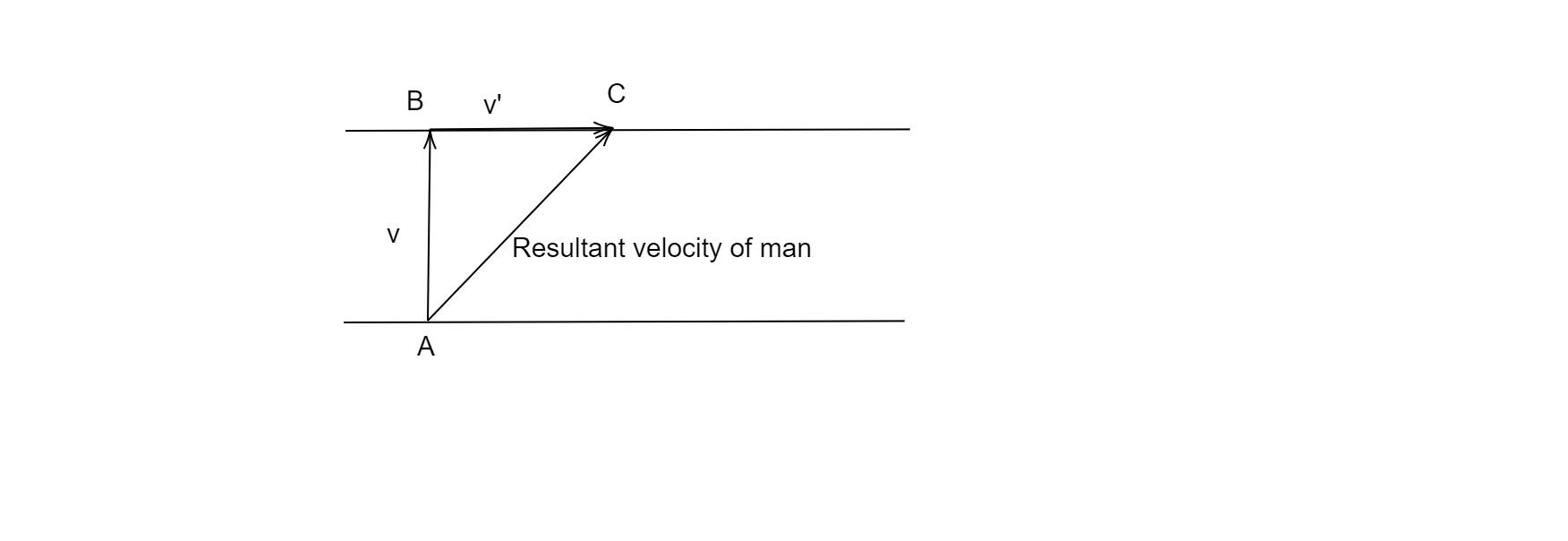As the river flows steadily and the swimmer makes his strokes, i.e., dives in the normal direction to the river current, i.e., swims in the normal direction to the flow of the river,
Let the time that the man takes to cross the river be $t$
The width of the river $(w = AB)$ is $1km$
The velocity of the man $(v)$ is $4km{h^{ - 1}}$
Therefore, $t = \dfrac{w}{v}$
$t = \dfrac{{1km}}{{4km{h^{ - 1}}}} = \dfrac{1}{4}hr = 0.25hr$
Since the river flows with a velocity $(v')$ of $3km{h^{ - 1}}$ and the man would also move along the direction of the flow of the river due to the speed of the river, given he would swim in the river for $0.25hr$.
Therefore, the distance $(d = BC)$ moved by the man in the direction of the flow of the river will be:
$\Rightarrow d = v' \times t$
$\Rightarrow d = 3km{h^{ - 1}} \times 0.25h$
$\Rightarrow d = 0.75km$
On converting the distance in kilometers $(km)$ to meters, $(m)$ we get:
$\Rightarrow d = 750m$
Therefore, the man went $750m$ in the direction of the river flow when he reached the river bank.

Note: We should focus on the time that the swimmer takes to cross the river and reach the other bank. The swimmer has to cross the river that time and at the same time moves in the direction of the flow of the river.