Solveeit Logo
Login

Question

Question: A man can swim in still water at \(4m/s\). River is flowing at \(2m/s\). The angle downstream at whi...

A man can swim in still water at 4m/s4m/s. River is flowing at 2m/s2m/s. The angle downstream at which he should swim to cross the river with minimum drift.
A) 120∘120^\circ
B) 150∘150^\circ
C) 30∘30^\circ
D) 60∘60^\circ

Explanation

Solution

If a man wants to cross the river with minimum drift then he must be reached at the point which is in front of his starting point. In this condition the drift is zero which is minimum drift.
Its means he should not have any velocity in the direction of river or opposite direction he must have velocity perpendicular to river flow

Complete step by step solution:
In our question the given values are vmr=4m/s{v_{mr}} = 4m/s and vrg=2m/s{v_{rg}} = 2m/s
Where vmr⇒{v_{mr}} \Rightarrow velocity of man with respect to river
And vrg⇒{v_{rg}} \Rightarrow velocity of river with respect to ground
If we see man from ground frame then see the diagram

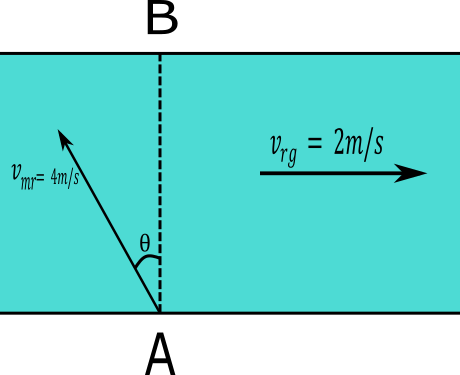
If man wants to reach at point B from point A then he should swim with an angle θ\theta with vertical direction or with y direction as mention in diagram
River flow in x direction with velocity 2m/s2m/s
Component of velocity of man with respect to river in x and y direction is 4sin⁡θ4\sin \theta and 4cos⁡θ4\cos \theta as and velocity of river is in x direction as shown in diagram.

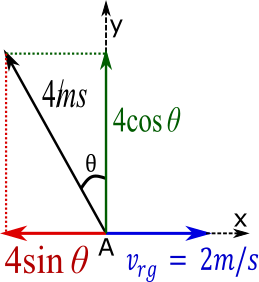
If man reached exactly at point B then the x component of velocity of man must equal to the velocity of the river.
⇒4sin⁡θ=2\Rightarrow 4\sin \theta = 2 Means net velocity in x direction must be zero.
⇒sin⁡θ=24\Rightarrow \sin \theta = \dfrac{2}{4}
⇒sin⁡θ=12\Rightarrow \sin \theta = \dfrac{1}{2}
So sin⁡θ=sin⁡30∘\sin \theta = \sin 30^\circ
∴θ=30∘\therefore \theta = 30^\circ
θ⇒\theta \Rightarrow Angle made from y direction
So angle made with downstream is =30∘+90∘= 30^\circ + 90^\circ
⇒120∘\Rightarrow 120^\circ
Hence the angle with downstream is 120∘120^\circ

Therefore, Option (A) is correct.

Note: Man has zero velocity in x direction means that the component of velocity of man in x direction must cancel out the velocity of river in x direction. Only in this condition man do not travel any distance along the river and can reach exactly the opposite point to the initial point. Means zero drift or minimum drift.