Question

A man can swim at a speed $2\,m/s$ in still water. He starts swimming in a river at an angle 150 to the direction of water flow and reaches the directly opposite point on the opposite Bank.
(a) Find the speed of flowing water.
(b) If the width of the river is $1\,km$ then calculate the time taken to cross the river.

Answer 1

Here the angle made by the man with the direction of flow is given as ${150^ \circ }$we can split that into ${90^ \circ }$ and ${60^ \circ }$.
By drawing the vector diagram we can get the value of velocity driven by taking sine of angle ${60^ \circ }$.
In order to find the value of time, the equation of velocity can be used.

Complete step-by-step solution:
It is given that a man can swim in still water at a speed $2\,m/s$
Let this velocity be denoted as ${V_m}$
Let the velocity of the river be denoted as ${V_R}$
(a) It is given that when the swimmer starts swimming at an angle 150 degree to the direction of water flow he reaches the directly opposite point of the bank.
let us try to draw the diagrammatic representation of the situation.

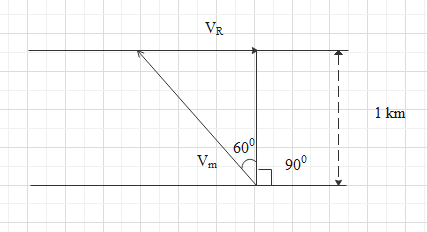
Total angle of the man is ${150^ \circ }$. We can split that into ${90^ \circ }$ and ${60^ \circ }$ as shown in the figure.
From the diagram we can see that the sine of the angle ${60^ \circ }$is obtained by dividing the velocity of the river by the velocity of man in still water.
since $\sin \,\theta$ is the ratio of opposite sides by hypotenuse.
$\sin \theta = \dfrac{{{\text{Opposite}}\,{\text{side }}}}{{{\text{Hypotenuse}}}}$
Here the velocity of the river forms the opposite side and the velocity of man is the hypotenuse .
Thus ,
$\sin \theta = \dfrac{{{V_R}}}{{{V_m}}}$
By substituting the given values we can find that the velocity of the river as
${V_R} = {V_m}\sin {60^ \circ }$
$\therefore {V_R} = 2 \times \dfrac{{\sqrt 3 }}{2} = \sqrt 3 \,m/s$
This is the speed of flowing water .
(b) We know that velocity is distance divided by time.
$v = \dfrac{d}{t}$
It is given that the width of the river is $1\,km = 1000\,m$ .
The component of velocity in the direction is ${V_m}\cos {60^ \circ }$
Therefore we can write
${V_m}\cos {60^ \circ } = \dfrac{{1000\,m}}{t}$
From this we can get the value of time as
$t = \dfrac{{1000}}{{2 \times \dfrac{1}{2}}}$
$\therefore t = 1000\,s$
This is the time taken to cross the river.

Note:- Here remember that while calculating the time taken we need to take the cos component of velocity. Since the width of the river is given to calculate the time we need to take the component of velocity in that direction. That is ${V_m}\cos {60^ \circ }$ .