Question

A man can row a boat with $4\;kmh^{-1}$ in still water. If he is crossing a river of width $4\;km$ where the current is $2\;kmh^{-1}$, in what direction should he head the boat if he wants to cross the river in the shortest time? What would be this minimum time?
A. Parallel to river current, 2hrs
B. Perpendicular to river current, 2hrs
C. Parallel to river current, 1 hr
D. Perpendicular to river current, 1 hr

Answer 1

Keep in mind that the man wants to cross the river in the shortest time. In this context, think of how the velocity of the river would maximize or minimize the velocity of the man, and how this would attribute the flow of the river current. In other words, think of how the man can gain a maximum velocity without compromising much on the distance covered. As for calculating the minimum once you find which component of his velocity will be the maximum (either the absolute or the relative velocities), calculating the time will be just a straightforward substitution.

Formula used:
Shortest time taken by the boat to travel the width of the river:
$t_{min} = \dfrac{d}{v_{max}}$, where d is the width of the river and $v_{max}$ is the boat’s maximum velocity, which is nothing but its relative velocity with water.

Complete answer:
Let us begin our computation, keeping in mind that the man wants to cross the river in the shortest time. This means that the man should head the boat in a direction perpendicular to the river current, since a component of the boat’s velocity is maximized when moving in a direction perpendicular to flow of river current and minimize the component of his velocity in the direction of the flow of river current.
Now, let us calculate the shortest time he takes to cross the river.
Now, the velocity of the man relative to the river is given as $V_{MR} = 4kmh^{-1}$
And the velocity of the river is given as $V_R = 2kmh^{-1}$
The width of the river is $d = 4\;km$

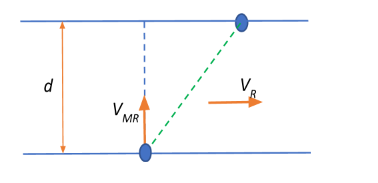
We consider only the relative velocity of the man with respect to the river since taking the shortest time implies directing all his velocity in the perpendicular direction.
Therefore, the minimum time taken by him to cross the river is by his maximum velocity component which is his velocity relative to the river:
$t_{min} = \dfrac{d}{v_{max}} = \dfrac{4}{4} = 1h$

So, the correct answer is “Option D”.

Note:
To cross the river by the shortest path, the boat should be rowed at an angle with respect to the river current direction since the relative velocity between the boat and the river is channelled towards covering the minimum distance, which is the width of the river. By moving at an angle, the boat can utilize the velocity of the flow of the river current to push it towards the shortest path.
To cover the shortest time, the boat needs to harness the maximum velocity it can get to travel the width of the river. The maximum velocity is given by the relative velocity of the boat w.r.t water since the river can add to the velocity of the boat in the perpendicular direction and minimize velocity in the direction of current flow.