Question

A man $A$ moves in the north direction with a speed $10\,m{s^{ - 1}}$ and man $B$ moves in ${30^ \circ }$ north of east with $10\,m{s^{ - 1}}$. Find the relative velocity of $B$ with respect to $A$?

Answer 1

In this problem, they have mentioned the direction of motion. So, we have to take the given information in vector form and then find the difference of two vector forms, and then the magnitude of the relative velocity of $B$ with respect to $A$ can be determined.

Complete step by step answer:
Given that,
The velocity of man $A$ is $10\,m{s^{ - 1}}$,
The man $A$ moves in north direction,
The velocity of man $B$ is $10\,m{s^{ - 1}}$,
The man $B$ moves in ${30^ \circ }$ north of east.

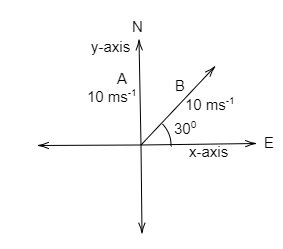
The man $A$ moves in the north direction and it is assumed as the y-axis, so the vector component of x-axis is assumed to be zero. Then, the velocity vector equation for man $A$ is,
${\vec v_A} = 0\hat i + 10\hat j\,.....................\left( 1 \right)$
The man $B$ move in ${30^ \circ }$ north of east, so in vector equation both the x-axis component and y-axis component is considered, then the velocity vector equation for man $B$ is,
${\vec v_B} = \left( {10\cos {{30}^ \circ }} \right)\hat i + \left( {10\sin {{30}^ \circ }} \right)\hat j\,........\left( 2 \right)$
From trigonometry, the value of $\cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2}$ and the value of $\sin {30^ \circ } = \dfrac{1}{2}$.
Substitute the both values of $\cos {30^ \circ }$ and $\sin {30^ \circ }$ in the equation (2), then the equation (2) is written as,
${\vec v_B} = \left( {10 \times \dfrac{{\sqrt 3 }}{2}} \right)\hat i + \left( {10 \times \dfrac{1}{2}} \right)\hat j$
On further simplification, the above equation is written as,
${\vec v_B} = \left( {5\sqrt 3 } \right)\hat i + 5\hat j\,............\left( 3 \right)$
To find the relative velocity of $B$ with respect to $A$,
${v_{BA}} = {\vec v_B} - {\vec v_A}$
On substituting the values of ${\vec v_B}$ and ${\vec v_A}$ in the above equation,
${v_{BA}} = \left( {\left( {5\sqrt 3 } \right)\hat i + 5\hat j} \right) - \left( {0\hat i + 10\hat j} \right)$
On subtracting, the above equation can be written as,
${\vec v_{BA}} = \left( {5\sqrt 3 } \right)\hat i - 5\hat j\,..................\left( 4 \right)$
To find the magnitude, take modulus on both sides, then,
$\left| {{{\vec v}_{BA}}} \right| = \left| {\left( {5\sqrt 3 } \right)\hat i - 5\hat j} \right|$
On further,
$\left| {{v_{BA}}} \right| = \sqrt {{{\left( {5\sqrt 3 } \right)}^2} + {{\left( { - 5} \right)}^2}}$
By square the terms inside the square root,
$\left| {{v_{BA}}} \right| = \sqrt {\left( {25 \times 3} \right) + 25}$
On simplifying the above equation,
$\left| {{v_{BA}}} \right| = \sqrt {75 + 25}$
On further,
$\left| {{v_{BA}}} \right| = \sqrt {100}$
By taking the square root,
$\left| {{v_{BA}}} \right| = 10\,m{s^{ - 1}}$

Thus, the relative velocity of the $B$ with respect to $A$ is ${v_{BA}} = 10\,m{s^{ - 1}}$.

Note:
In this solution we have to remember two important steps, one is the velocity vector equation for the man $B$, which contains sine and cosine because the man $B$ moves in some angle. And another important step is while subtracting the two vectors, the x-axis component is subtracted with x-axis component only, similarly for y-axis also. So, these two steps are important while solving this problem.