Question
Question: A man 2m tall, walks at the rate of \(1\dfrac{2}{3}m/sec\) towards a street light which is \(5\dfrac...
A man 2m tall, walks at the rate of 132m/sec towards a street light which is 531m above the ground. At what rate is the tip of his shadow moving? At what rate is the length of his shadow changing when he is 331m from the base of the light?
Solution
We are going to solve this problem by proving both the triangles similar and then we will differentiate the rate of change shadow with respect to time.
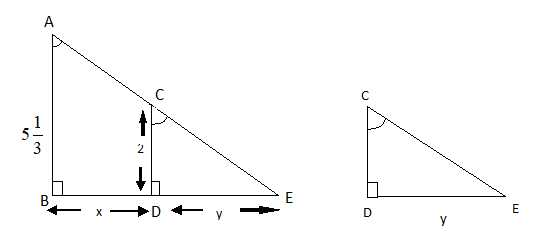
∠ABE and∠CDE=90∘.
∠A=∠C (Angles on the same side of a triangle are equal)
AB∥CD
Hence, ΔABE and ΔCDE are similar triangles.
So, similar triangles have their corresponding sides in proportion are equal CDAB=DEBE=CEAE
Formula Used:
For finding the rate of changes in shadow we will differentiate it with respect to time =dtdx and dtdy
Complete step by step answer:
Suppose AB is the height of the street light, and CD is the height of the man. Suppose at any time t the man CD is at a distance x meter from the street light. y is the shadow of the man.
So, the rate of change of the distance of man at time t is dtdx=231m/s
We know that,
∠ABE and ∠CDE are equal, because both are the right angle.
ΔADE and ΔCDE are similar triangle
Hence, CDAB=DEBE=CEAE as sides of similar triangles are equal.
It is given that CD=2m and AB=531=316m
From the diagram, we can conclude, BD=x, DE=y, and BE=x+y
So putting the values of AB, BE, DE, CD in the above equation:
⇒12316=yx+y
Simplifying the above equation we get,
⇒616=yx+y
Cross multiply the denominator to the numerator to solve the above equation,
⇒16y=6(x+y)
⇒16y=6x+6y
Arranging the same variables in the above equation,
⇒16y−6y=6x
⇒10y=6x
Now, we will find the rate of change of shadow. We will differentiate the rate of change of shadow with respect to time t.
⇒10dtdy=6dtdx
Value of dtdx is given = 35
⇒10dtdy=6×35
Simplifying we get,
⇒dtdy=10×36×5
Multiplying the terms,
⇒dtdy=3030=1
So, the rate of change of shadow dtdy is 1
Now, we have to find out the rate at which the tip of the shadow CE changes.
AB=316
We have to find the rate at which BE=BD+DE moves
From similar property = CDAB=DEBE
Let BE=P
Now putting the values of AB, CD, DE in the above equation
⇒12316=yP
Simplifying we get,
⇒38=yP
Solving for P,
⇒38y=P
Now differentiating it with respect to time t,
⇒38×dtdy=dtdP
Now putting the value of dtdy=1 in the above equation
⇒dtdP=38 is the rate at which the tip of the shadow changes.
Therefore, the rate of change in shadow length is 38.
Note:
From the similar property of the triangle, we will take the sides in proportion in equal and find out the changes in the rate of the shadow and the tip of the shadow. In general, these real-life problems convert the problem into a diagram. It is easy to understand the problem to find and it will make the problem easiest to solve.
