Question

A man $2m$ tall walks at rate $1\dfrac{2}{3}$ meters per second towards a street light which is $5\dfrac{1}{3}m$ above the ground. At what rate is the tip of his shadow moving? At what rate is the length of shadow changing when it is $3\dfrac{1}{3}m$ away from the base of the light?

Answer 1

The given question belongs to the height and distances concept of trigonometry domain. In the problem, a man is walking towards a street light and a shadow is formed behind him. The speed of man is given in the question. So, we first draw a figure to represent the situation and understand the problem more clearly. We introduce some variables for the length of shadow and distance between man and street light and form a relation between them. Then, we differentiate the equation and get to the final answer.

Complete step by step solution:
So, the height of the man is $2m$ .
The height of the street light is $5\dfrac{1}{3}m = \dfrac{{16}}{3}m$ .
Now, let us assume the distance of man from the street light as x meters.
Also, the distance from the end of the shadow to the street light is y metres.
So, the situation can be represented as in the figure below:

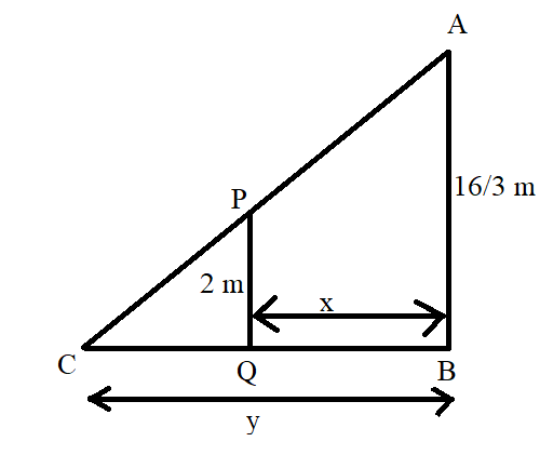
Now, we know that $\angle PCQ = \angle ACB$ as both the angles are the same.
So, the tangent of the angle is equal to $\dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$. So, we get,
$\Rightarrow \dfrac{2}{{y - x}} = \dfrac{{16}}{{3y}}$
Cross multiplying the terms and cancelling the common factors in both sides of the fraction, we get,
$\Rightarrow \dfrac{2}{{y - x}} = \dfrac{{16}}{{3y}}$
$\Rightarrow 3y = 8y - 8x$
Shifting the like terms together, we get,
$\Rightarrow 5y = 8x$
Now, differentiating both the sides of the equation, we get,
$\Rightarrow 5\dfrac{{dy}}{{dt}} = 8\dfrac{{dx}}{{dt}} - - - - - \left( 1 \right)$
Now, we are given that the man is walking towards the street light at a rate of $1\dfrac{2}{3} = \dfrac{5}{3}$ meters per second.
So, we have, $\dfrac{{dx}}{{dt}} = \dfrac{5}{3}$ .
We have to calculate the rate at which the tip of man’s shadow is moving and the rate at which the length of the shadow is decreasing.
So , the rate at which the man’s shadow is moving is $\dfrac{{dy}}{{dt}}$ .
From equation $\left( 1 \right)$ , we get,
$\Rightarrow 5\dfrac{{dy}}{{dt}} = 8\left( {\dfrac{5}{3}} \right)$
So, we get the value of $\dfrac{{dy}}{{dt}}$ as,
$\Rightarrow \dfrac{{dy}}{{dt}} = \dfrac{8}{3}$
Hence, the rate at which the tip of man’s shadow is moving is $\dfrac{8}{3}$ meters per second.
Now, we know that the length of the shadow is $\left( {y - x} \right)$ .
So, rate at which length of man’s shadow is changing is $\dfrac{{d\left( {y - x} \right)}}{{dt}} = \dfrac{{dy}}{{dt}} - \dfrac{{dx}}{{dt}}$ .
So, we get, $\dfrac{{dy}}{{dt}} - \dfrac{{dx}}{{dt}} = \left( {\dfrac{8}{3} - \dfrac{5}{3}} \right)$
$\Rightarrow \dfrac{{dy}}{{dt}} - \dfrac{{dx}}{{dt}} = 1$
Hence, the rate at which the length of shadow changes is $1$ metres per second.
So, the correct answer is “ $1$ metres per second”.

Note : We should have a strong grip over the concepts of trigonometry and height and distances in order to deal with such kinds of problems. We should have accuracy in calculations, derivatives and arithmetic in order to be sure of the final answer. We must know that there may be additional information given in the question that is not of use in solving the problem like the distance of man from the street light in the above problem.