Question

A man 2 metres high walks at a uniform speed of 5km/hr away from a lamp post 6 metres high. Find the rate at which the length of his shadow increases.

Answer 1

Hint: Assume that the angle made by the BE with AE be $\theta$ . Use the fact that in a right-angled triangle the ratio of the opposite side to the adjacent side is the tangent of the angle. Hence prove that $CE=CD\cot \theta$ . Use the fact that the triangle ABE and DCE are similar and hence prove that $\dfrac{AB}{DC}=\dfrac{AE}{CE}$ and hence find the length AC. Differentiate with respect to t and hence find the value of $\dfrac{d\theta }{dt}$ . Differentiate the expression of CE to and substitute the value of $\dfrac{d\theta }{dt}$ and hence find the speed of the shadow.

Complete step-by-step answer:

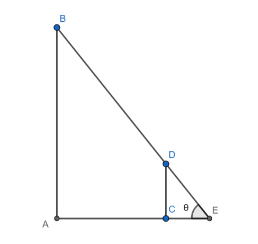
Given: A lamppost AB of height 6 metres and a man DC of height 2 metres is moving away from the post with speed of 5 metres per second.
To determine: The speed of the head of the shadow E.
Let $\angle DEC=\theta$
In triangle EDC, we have DC is the side opposite to E and CE is the side adjacent to E.
Hence, we have
$\tan \theta =\dfrac{DC}{CE}$
Multiplying both sides by CE and dividing both sides by $\tan \theta$ , we get
$CE=DC\cot \theta$
Differentiating with respect to t(time), we get
$\dfrac{d\left( CE \right)}{dt}=-DC{{\csc }^{2}}\theta \dfrac{d\theta }{dt}\text{ }\left( i \right)$
Similarly in triangle ABE, we have
$AE=AB\cot \theta$
Also, we have triangle ABE and DCE are similar (Since AB||DC).
Hence, we have
$\dfrac{AB}{DC}=\dfrac{AE}{CE}$ (Ratios of corresponding sides of two similar triangles is same)
$\begin{aligned} & \dfrac{6}{2}=\dfrac{AE}{CE} \\\ & \Rightarrow AE=3CE \\\ \end{aligned}$
Hence, we have
$AC=2CE=4\cot \theta$
Hence, we have
$\dfrac{d\left( AC \right)}{dt}=-4{{\csc }^{2}}\theta \dfrac{d\theta }{dt}$
Since the person moves with velocity of $5m{{s}^{-1}}$ , we have
$\dfrac{d\left( AC \right)}{dt}=5$
Hence, we have
${{\csc }^{2}}\theta \dfrac{d\theta }{dt}=\dfrac{-5}{4}$
Substituting in equation (i), we get
$\dfrac{d\left( CE \right)}{dt}=-2\left( \dfrac{-5}{4} \right)=\dfrac{5}{2}m{{s}^{-1}}$
Hence the speed of the shadow is $\dfrac{5}{2}m{{s}^{-1}}$ .

Note: Instead of trigonometry, we can also use simple geometry to solve the question.
We have
$\begin{aligned} & \dfrac{AB}{AE}=\dfrac{DC}{CE} \\\ & \Rightarrow AE=\dfrac{6CE}{2}=3CE \\\ \end{aligned}$
Hence, we have
$AC=2CE$
Differentiating both sides with respect to t, we get
$\begin{aligned} & \dfrac{d\left( AC \right)}{dt}=2\times \dfrac{d\left( CE \right)}{dt} \\\ & \Rightarrow \dfrac{d\left( CE \right)}{dt}=\dfrac{5}{2} \\\ \end{aligned}$
Which is the same as obtained above.