Question

A man 2 m tall, whose eye level is $1.84 m$ above the ground, looks at his image in a vertical mirror. What is the minimum vertical length of the mirror if the man is able to see the whole of himself?
A. $0.5 m$
B. $0.92 m$
C. $1 m$
D. $1.84 m$

Answer 1

According to one of the laws of reflection, the normal line divides the incidence angle and reflection angle equally. Use this fact to draw the ray diagram of the image formation of the man by the plane mirror. Recall the properties of the similar triangles and determine the required height of the mirror so that the man can see the whole of himself in the mirror.

Complete step by step answer:
To answer this question, we have to discuss the law of reflection. According to one of the laws of reflection, the normal divides the incidence angle and reflection angle equally.

Now, let’s consider the following ray diagram.

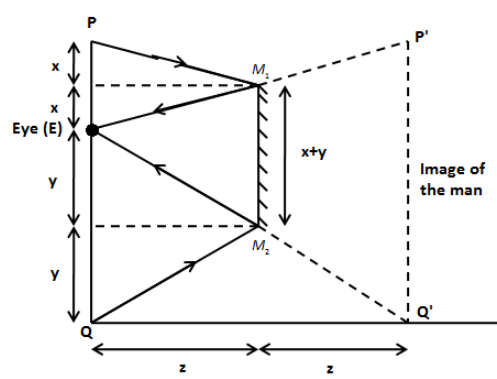
In the above figure, we can observe that $\Delta E{M_1}{M_2}$ and $\Delta EP'Q'$ are similar triangles. From the property of similar triangles, we can write,
$\dfrac{{{M_1}{M_2}}}{{P'Q'}} = \dfrac{z}{{2z}}$
$\Rightarrow {M_1}{M_2} = \dfrac{{P'Q'}}{2}$
Here, ${M_1}{M_2}$ is the height of the plane mirror.

From the above figure, we have, $P'Q' = PQ$ which is the total height of the man. Therefore,
${M_1}{M_2} = \dfrac{{PQ}}{2}$
Substituting $PQ = 2\,{\text{m}}$ in the above equation, we get,
${M_1}{M_2} = \dfrac{2}{2}$
$\therefore {M_1}{M_2} = 1\,{\text{m}}$
Therefore, the required vertical height of the plane mirror should be 1 m so that the man can see the whole of himself in the mirror.

So, the correct answer is C.

Note: To answer this question we have used the law of reflection. So, even if the mirror is held such that the upper edge of the mirror is parallel to our eye, we can see our head in the mirror. Remember, for the plane mirror, the image distance and object distance are the same and therefore, we have mentioned the distance of the man from the mirror and distance of image of the man by the same letter z.