Question

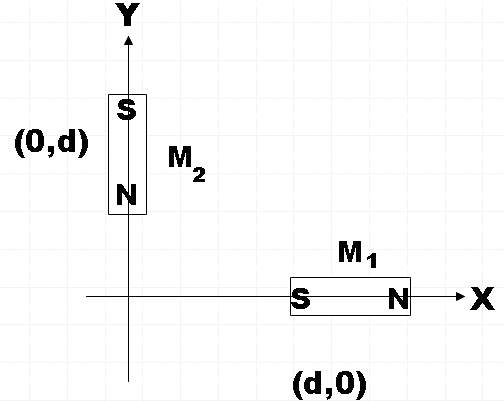
A magnetic needle is arranged at origin with two bar magnets of magnetic moments M, 2M arranged with coordinates of their centers (d, 0) and ( 0, d) as shown. Then find the unit vector pointing along the direction of the magnetic needle in equilibrium.

A. $\dfrac{1}{\sqrt{5}}\widehat{i}-\dfrac{2}{\sqrt{5}}\widehat{j}$
B. $\dfrac{2}{\sqrt{5}}\widehat{i}-\dfrac{1}{\sqrt{5}}\widehat{j}$
C.$\dfrac{1}{\sqrt{2}}\widehat{i}+\dfrac{1}{\sqrt{2}}\widehat{j}$
D.$\dfrac{2}{\sqrt{3}}\widehat{i}+\dfrac{1}{\sqrt{3}}\widehat{j}$

Answer 1

As a first step, you could recall the expression for the magnetic field at an axial point due to a bar magnet. Then, you could assign the direction of these fields accordingly by remembering that the magnetic needle always directs in the direction of the north pole. Now, find the unit vector by dividing the net magnetic field at origin by its magnitude.

Formula used:
Magnetic field at axial point,
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2m}{{{d}^{3}}}$

Complete Step by step solution:
In the question, we are given two bar magnets that are with magnetic moments M and 2M that are arranged exactly as shown in the above figure with their respective centers at $\left( d,0 \right)$ and $\left( 0,d \right)$. We are keeping a magnetic needle at the origin and we are asked to find the unit vector along the direction at which the magnetic field will point at equilibrium.
From the figure, we see that the origin is the axial point to both the given bar magnets.
Now, let us recall the expression for magnetic field due to a bar magnet at its axial point which is given by,
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2m}{{{d}^{3}}}$
Where, m is the magnetic moment and d is the distance of the magnet’s centre from the considered point.
The magnetic field due to the bar magnet ${{M}_{1}}$of magnetic moment M is given by,
${{B}_{1}}=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{d}^{3}}}\widehat{i}$………………………………………………………. (1)
As the magnetic needle always points in the direction of north pole of the magnet, the field would be in positive x direction.
Now, the magnetic field due to the bar magnet ${{M}_{2}}$of magnetic moment 2M is given by,
${{B}_{2}}=-\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2\left( 2M \right)}{{{d}^{3}}}\widehat{j}$………………………………………………………. (2)
The field would be directed in the direction of the north pole which would be in negative y direction.
The net magnetic field at origin would be the sum of (1) and (2),
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{d}^{3}}}\widehat{i}+-\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2\left( 2M \right)}{{{d}^{3}}}\widehat{j}$ ……………………………………………………. (3)
Now you may recall that the unit vector for given vector is given by,
$\widehat{B}=\dfrac{\overrightarrow{B}}{\left| B \right|}$ ……………………………………………………. (4)
Where, $\left| B \right|$ would be the magnitude of the given magnetic field.
$\left| B \right|=\sqrt{{{\left( \dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{d}^{3}}} \right)}^{2}}+{{\left( \dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2\left( 2M \right)}{{{d}^{3}}} \right)}^{2}}}$
$\Rightarrow \left| B \right|=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{d}^{3}}}\sqrt{1+4}$
$\therefore \left| B \right|=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{d}^{3}}}\sqrt{5}$ ……………………………………………………. (5)
Substituting (3) and (5) in (4), we get,
$\widehat{B}=\dfrac{\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{d}^{3}}}\widehat{i}}{\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{d}^{3}}}\sqrt{5}}+\dfrac{-\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2\left( 2M \right)}{{{d}^{3}}}\widehat{j}}{\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{d}^{3}}}\sqrt{5}}$
$\therefore \widehat{B}=\dfrac{1}{\sqrt{5}}\widehat{i}-\dfrac{2}{\sqrt{5}}\widehat{j}$
Therefore, we found the unit vector pointing in the direction of magnetic needle in equilibrium to be,
$\widehat{B}=\dfrac{1}{\sqrt{5}}\widehat{i}-\dfrac{2}{\sqrt{5}}\widehat{j}$

Hence, option A is found to be the correct answer.

Note:
We have discussed the case of the magnetic field in terms of magnetic moment for an axial point. Now for the case of an equilateral point the expression would look something like this,
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m}{{{d}^{3}}}$
Therefore, we see that the magnetic field at an axial point is twice that at an equilateral point.