Question

A magnetic field due to a long straight wire carrying a current $I$ is proportional to
A. $I$
B. ${I^2}$
C. ${I^3}$
D. $\sqrt I$

Answer 1

Apply Biot- savart’s law by considering an elementary length on the finite straight wire. For the long or infinite length of the straight wire or any conductor, the perpendicular distance from the wire is at the center of the wire that ${\phi _1} = {\phi _2} = 90^\circ$.

Complete step by step solution:
Let us consider an straight wire through which current $I$ flows and a point $P$, which lies at a perpendicular distance $a$ from the wire as shown in the diagram below:

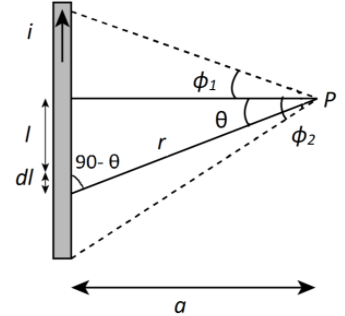
Now let $dl$ be a small current carrying element at distance $r$ from the point $P$ and the angle between distances $r$ and $a$ be $\theta$. The length between the center of the wire and elementary length is $l$.
Now we apply Bio- savart’s law, the magnetic field due to the current element $dl\;$ at point $P$ is,
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idl\sin \left( {90^\circ - \theta } \right)}}{{{r^2}}}$ … (I)
From the triangle formed by $r,\;a\;{\rm{and}}\;l$,
$r = \dfrac{a}{{\cos \theta }}$ … (II)
And
$l = a\tan \theta$
Now differentiate above equation with respect to $\theta$, we get,
$\dfrac{{dl}}{{d\theta }} = a{\sec ^2}\theta$
$\Rightarrow dl = a{\sec ^2}\theta d\theta$ … (III)

Now we substitute the values of $dl$ and $r$ using equation (II) and (III), we have,
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I\left( {a{{\sec }^2}\theta d\theta } \right)\cos \theta }}{{{{\left( {\dfrac{a}{{\cos \theta }}} \right)}^2}}}\\\ \Rightarrow dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Id\theta \cos \theta }}{a}$
Now we integrate from $- {\phi _1}$ to ${\phi _2}$ the above equation,

$$\int\limits_0^B {dB} = \int\limits_{ - {\phi _1}}^{{\phi _2}} {\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Id\theta \cos \theta }}{a}} \\\ \Rightarrow B - 0 = \dfrac{{{\mu _0}I}}{{4\pi a}}\int\limits_{ - {\phi _1}}^{{\phi _2}} {\cos \theta d\theta }$$

After further simplifying, we get,

$$B = \dfrac{{{\mu _0}I}}{{4\pi a}}\left[ {\sin \theta } \right]_{ - {\phi _1}}^{{\phi _2}}\\\ \Rightarrow B = \dfrac{{{\mu _0}I}}{{4\pi a}}\left( {\sin {\phi _2} + \sin {\phi _1}} \right)$$

It is given in the question that the straight wire is long that is infinite, in this the point $P$ always be at the center of the straight wire. So, the angle ${\phi _1}$ and ${\phi _2}$ will be equal to $90^\circ$.

Now substitute ${\phi _1}$ and ${\phi _2}$ as $90^\circ$in the above expression.

$$B = \dfrac{{{\mu _0}I}}{{4\pi a}}\left( {\sin 90^\circ + \sin 90^\circ } \right)\\\ \Rightarrow B = \dfrac{{{\mu _0}I}}{{4\pi a}}\left( 2 \right)\\\ \Rightarrow B = \dfrac{{{\mu _0}I}}{{2\pi a}}$$

Since $\dfrac{{{\mu _0}}}{{2\pi }}$ is a constant quantity, so the above expression can be written as,
$B \propto \dfrac{I}{a}$
Thus, the magnetic field ($B$) due to a long straight wire carrying a current ($I$) is proportional to $I$

So, the correct answer is “Option A”.

Note:
Be careful while answering because the formula for finite straight wire and infinite straight is completely different.
When wire has finite length: $B = \dfrac{{{\mu _0}I}}{{4\pi a}}\left( {\sin {\phi _2} + \sin {\phi _1}} \right)$
When wire has infinite length, ${\phi _1} = {\phi _2} = 90^\circ$: $B = \dfrac{{{\mu _0}I}}{{2\pi a}}$
When wire has infinite length and point $P$ lies at near wire’s end, ${\phi _1} = 90^\circ \;{\rm{and}}\;{\phi _2} = 0$:
$B = \dfrac{{{\mu _0}I}}{{4\pi a}}$