Question

A magnetic field directed along Z axis varies as $B = \dfrac{{{B_0}x}}{a}$, where ${B_0} = 2\,{\text{tesla}}$ and $a = 1\,{\text{m}}$. A conducting square loop of side is placed with its edges parallel to X and Y axes. If the loop is made to move with a constant velocity ${v_0} = 6\,{\text{m/s}}$ directed along X axis, the induced emf (in volts) in the loop is:

Answer 1

Use the formula for the flux of the loop and the emf induced in the loop. These equations give the relation between the induced emf, magnetic field, length of the loop and velocity of the loop.

Formulae used:

The magnetic flux $\phi$ of a moving loop is
$\phi = BA$ …… (1)

Here, $B$ is the magnetic field and $A$ is the area of the loop.

The induced emf $e$ is given by
$e = \dfrac{{d\phi }}{{dt}}$ …… (2)

Here, $d\phi$ is the change in the magnetic flux in the time $dt$.

Complete step by step answer: The conducting square loop placed with its edges parallel to X and Y axes is placed in a magnetic field $B = \dfrac{{{B_0}x}}{a}$ directed along Z axis with ${B_0} = 2\,{\text{tesla}}$ and $a = 1\,{\text{m}}$. The velocity of this moving loop is ${v_0} = 6\,{\text{m/s}}$.

The diagram for the given square loop moving in the magnetic field is as follows:

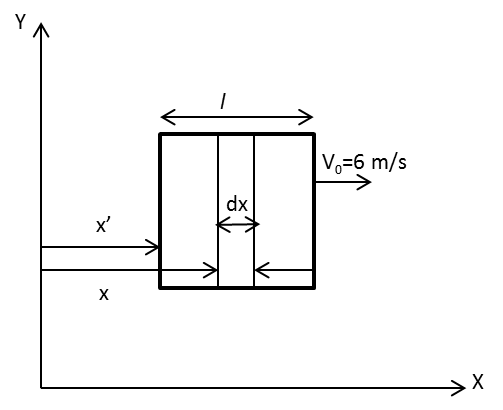
Let $x$ is the initial position of the loop and $x'$ is the changed position of the loop. $dx$ is the change in the position of the loop.

Calculate the magnetic flux of the loop for the change $dx$.

Rewrite the equation (1) for the small magnetic flux of the loop.
$d\phi = Bldx$

Take integration on both sides of the above equation to calculate the total magnetic flux.
$\int {d\phi } = \int {Bldx}$
$\Rightarrow \phi = \int {Bldx}$

Substitute $\dfrac{{{B_0}x}}{a}$ for $B$ in the above equation and take the integration from $x'$ to $x' + l$.
$\phi = \int\limits_{x'}^{x' + l} {\dfrac{{{B_0}x}}{a}ldx}$
$\Rightarrow \phi = \dfrac{{{B_0}l}}{a}\int\limits_{x'}^{x' + l} {xdx}$
$\Rightarrow \phi = \dfrac{{{B_0}l}}{a}\left[ {\dfrac{{{x^2}}}{2}} \right]_{x'}^{x' + l}$
$\Rightarrow \phi = \dfrac{{{B_0}l}}{{2a}}\left[ {{{\left( {x' + l} \right)}^2} - x{'^2}} \right]$

Now, calculate the emf induced in the loop.

The change in the position $x'$ with respect to the time $t$ is the velocity of the loop.
${v_0} = \dfrac{{dx'}}{{dt}}$

Substitute $\dfrac{{{B_0}l}}{{2a}}\left[ {{{\left( {x' + l} \right)}^2} - x{'^2}} \right]$ for $\phi$ in equation (2).
$e = \dfrac{{d\left[ {\dfrac{{{B_0}l}}{{2a}}\left[ {{{\left( {x' + l} \right)}^2} - x{'^2}} \right]} \right]}}{{dt}}$
$\Rightarrow e = \dfrac{{{B_0}l}}{{2a}}\dfrac{{d\left[ {\left[ {{{\left( {x' + l} \right)}^2} - x{'^2}} \right]} \right]}}{{dt}}$
$\Rightarrow e = \dfrac{{{B_0}l}}{{2a}}\left[ {2\left( {x' + l} \right)\dfrac{{dx'}}{{dt}} - 2x'\dfrac{{dx'}}{{dt}}} \right]$

Substitute ${v_0}$ for $\dfrac{{dx'}}{{dt}}$ in the above equation.
$\Rightarrow e = \dfrac{{{B_0}l}}{{2a}}\left[ {2\left( {x' + l} \right){v_0} - 2x'{v_0}} \right]$

Suppose the original position $x'$ of the loop is at the origin.

Substitute $0\,{\text{m}}$ for $x'$ in the above equation.
$e = \dfrac{{{B_0}l}}{{2a}}\left[ {2\left( {0\,{\text{m}} + l} \right){v_0} - 2\left( {0\,{\text{m}}} \right){v_0}} \right]$
$\Rightarrow e = \dfrac{{{B_0}l}}{{2a}}\left[ {2{v_0}l} \right]$
$\Rightarrow e = \dfrac{{{B_0}{v_0}{l^2}}}{a}$

Substitute $2\,{\text{T}}$ for ${B_0}$, $6\,{\text{m/s}}$ for ${v_0}$, $\dfrac{1}{2}\,{\text{m}}$ for $l$ and $1\,{\text{m}}$ for $a$ in the above equation.
$e = \dfrac{{\left( {2\,{\text{T}}} \right)\left( {6\,{\text{m/s}}} \right){{\left( {\dfrac{1}{2}\,{\text{m}}} \right)}^2}}}{{\left( {1\,{\text{m}}} \right)}}$
$\Rightarrow e = 3\,{\text{V}}$

Hence, the induced emf in the loop is $3\,{\text{V}}$.

Note: Since all the units used in the equation are in the SI system of units, the unit of the induced emf is ultimately in volts (in the SI system of units).