Solveeit Logo
Login

Question

Question: A magnet of dipole moment \(2\; Am^2\) is deflected through \(30^{\circ}\) from magnetic meridian. T...

A magnet of dipole moment 2  Am22\; Am^2 is deflected through 30∘30^{\circ} from magnetic meridian. The required deflecting torque is (BH=0.4×10−4  T)({B}_{H}=0.4\times 10^{-4}\; T):
A.)0.4×10−40.4\times 10^{-4} Nm
B.)0.4 Nm
C.)0.2×10−40.2\times 10^{-4} Nm
D.)None of these

Explanation

Solution

Hint: The torque required can be calculated by the cross product of the magnet dipole moment and horizontal component of magnetic meridian as there is no presence of any other magnetic field.

Formula used:
Torque, τ=μ⃗×BH⃗\tau=\vec{\mu} \times \vec{{B}_{H}}, where μ\mu is the magnets dipole moment and BH{B}_{H} is the horizontal component of Earth’s magnetic field.

Complete step by step solution:
We have been given that the dipole moment of the magnet, μ=2  Am2\mu=2\; Am^2 and the horizontal component of the Earth’s magnetic field is BH=0.4×10−4  T{B}_{H}=0.4\times 10^{-4}\; T.
It is also given that the angle between the magnet and the magnetic meridian is 30∘30^{\circ}. So, we can illustrate the condition as follow

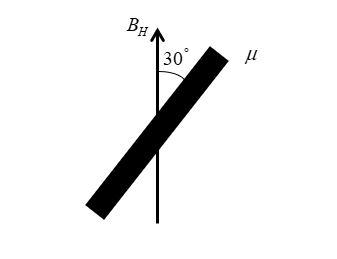
Now, we can find the torque generated by using the formula τ=μ⃗×BH⃗=μBHsinθ\tau=\vec{\mu} \times \vec{{B}_{H}}=\mu {B}_{H} sin\theta, where μ\mu is the magnets dipole moment, BH{B}_{H} is the horizontal component of Earth’s magnetic field and θ\theta is the angle between the magnet and the magnetic meridian.

Therefore, τ=2×0.4×10−4sin30∘=0.82×10−4=0.4×10−4Nm\tau=2 \times 0.4\times 10^{-4} sin30^{\circ}=\dfrac{0.8}{2}\times 10^{-4}=0.4\times 10^{-4} Nm
Hence, option a is the correct answer.

Additional information:
An imaginary line that connects the magnetic north and south poles of the Earth is called a magnetic meridian. A compass needle when suspended freely on the Earth’s surface align itself parallel to the magnetic meridian. although there is some hindrance in their alignment due to the east to west longitude which become complete geodesic and thus magnetic declination comes into picture.

Note:
The orientation of the magnet or say its inclination changes as we move from equator to the poles and is called the angle of dip. This dip is caused by both horizontal and vertical components of the magnetic field. At poles, this dip is 90∘90^{\circ} and at the equator, the dip is 0∘0^\circ.