Solveeit Logo
Login

Question

Question: A magnet 10 cm long and having pole strength 2 amp m is deflected through \({{30}^{\circ }}\) from t...

A magnet 10 cm long and having pole strength 2 amp m is deflected through 30∘{{30}^{\circ }} from the magnetic meridian. The horizontal component of the Earth's induction is 0.32×10−40.32\times {{10}^{-4}} tesla then the value of the deflecting couple is
a)32×10−7Nm b)16×10−7Nm c)64×10−7Nm d)48×10−7Nm \begin{aligned} & a)32\times {{10}^{-7}}Nm \\\ & b)16\times {{10}^{-7}}Nm \\\ & c)64\times {{10}^{-7}}Nm \\\ & d)48\times {{10}^{-7}}Nm \\\ \end{aligned}

Explanation

Solution

The deflecting couple is the torque acting on the magnet due to the horizontal component of the Earth’s magnetic field. When a magnet is placed in a magnetic field the torque acting on that magnet is given by, τ=m×B\tau =m\times B where m is the magnetic moment of the magnet and B is the magnetic field in which the magnet is kept. The above expression can also be written as, τ=mBSin⁡θ\tau =mB\operatorname{Sin}\theta where θ\theta is the angle between the magnetic field B and the magnetic moment. Hence from this we can calculate the value of the deflecting couple.

Complete step by step answer:

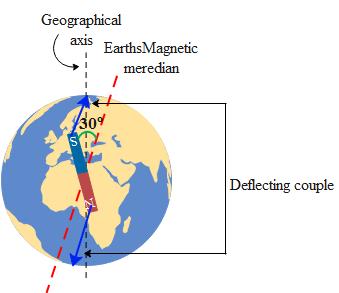
In the above figure we can see the magnet is making 30 degrees with respect to the magnetic ,meridian. The deflecting couple is depicted by the blue arrows in the diagram. Hence the torques on the magnet are given by, τ=mBSin⁡θ...(1)\tau =mB\operatorname{Sin}\theta ...(1). The magnetic moment of the magnet is the product of pole strength (p) times the length (l) of the bar magnet. Hence the magnetic moment of the above magnet is,
m=p(l)=2(10×10−2)=20×10−2 amp m2m=p(l)=2(10\times {{10}^{-2}})=\text{20}\times {{10}^{-2}}\text{ amp }{{\text{m}}^{\text{2}}}. Hence substituting this in equation (1) we get,
τ=mBSin⁡θ τ=20×10−2(0.32×10−4)Sin⁡30∘,sinceSin⁡30∘=12 τ=6.4×10−62 τ=32×10−7Nm \begin{aligned} & \tau =mB\operatorname{Sin}\theta \\\ & \tau =20\times {{10}^{-2}}(0.32\times {{10}^{-4}})\operatorname{Sin}{{30}^{\circ }},\text{since}\operatorname{Sin}{{30}^{\circ }}=\dfrac{1}{2} \\\ & \tau =\dfrac{6.4\times {{10}^{-6}}}{2} \\\ & \tau =32\times {{10}^{-7}}Nm \\\ \end{aligned}
Hence the correct answer to the above question is option a.

Note:
It is to be noted that along the Earth's meridian, the horizontal components of the Earth’s magnetic field is to be considered. This is because there does not exist the vertical component along the Earth's meridian. It is also to be noted that the geographical axis and the Earth’s meridian are oriented differently. Therefore the magnetic north and the geographical north vary slightly. Also it is also to be noted that the geographical poles of the earth are different from the magnetic poles of the Earth.