Question

A luminous object is placed at a distance of 30 cm from the convex lens of focal length 20 cm. On the other side of the lens, at what distance from the lens a convex mirror of radius of curvature 10 cm be placed in order to have an upright image of the object coincident with it?
A) 60 cm
B) 50 cm
C) 30 cm
D) 20 cm

Answer 1

A convex lens is an optical lens made up of two spherical surfaces curved outwards. A convex lens converges the rays of light that are incident on its surface parallel to the principal axis. It forms a virtual image when the object is placed in front of the focal point. The image formed is magnified and upright.

Complete step by step answer:
Step I:
Given object distance, $u = -30cm$.
[Since in convex lens object is placed in front of the lens, so the value of u is negative]
Focal length, $f =20cm$
Step II:
In order to obtain the image coincident with an object, the image of the object from the convex lens after refraction must be formed on the center of the curvature of the convex mirror.

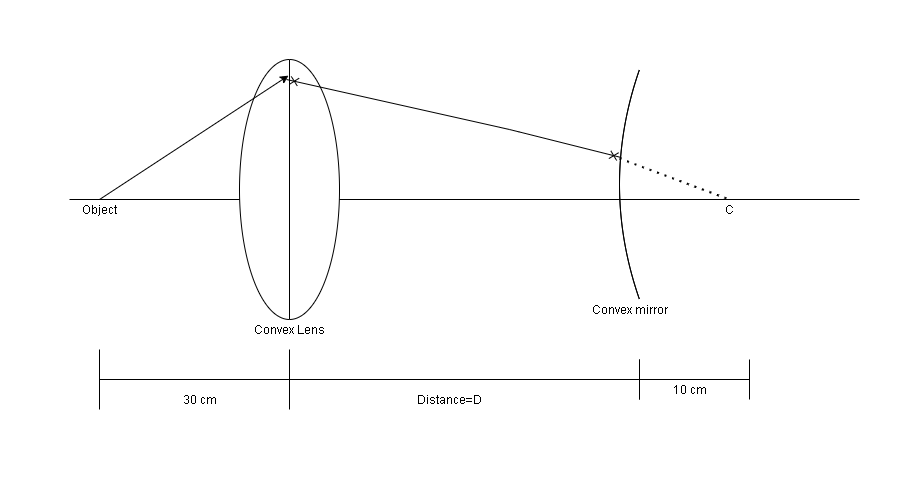
The distance of an image from a convex lens after refraction from it can be calculated using the lens formula. The lens formula is
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
$\dfrac{1}{v} = \dfrac{1}{u} + \dfrac{1}{f}$
$\dfrac{1}{{ - 30}} + \dfrac{1}{{20}} = \dfrac{1}{v}$
Solving above equation,
$v = 60cm$
Step III:
Image is formed at a distance of 60 cm from the lens.
Thus convex mirror should be kept at a distance of $60 - 10 = 50cm$

$\therefore$ The convex mirror should be kept at a distance of 50cm. Hence, option B is the correct answer.

Note:
A convex mirror is placed on the other side of the convex lens and an upright image is to be obtained. So for a convex mirror, the nature of the image formed is always upright. When the object is placed far away from the convex mirror then the image formed will be virtual and upright located at the focal point of the mirror.