Question

A luminous object is placed at a distance of 30 cm from the convex lens of focal length 20 cm. On the other side of the lens, at what distance from the lens a convex mirror of radius of curvature 10 cm be placed to have an upright image of the object coincident with it?
A) 30 cm
B) 60 cm
C) 50 cm
D) 12 cm

Answer 1

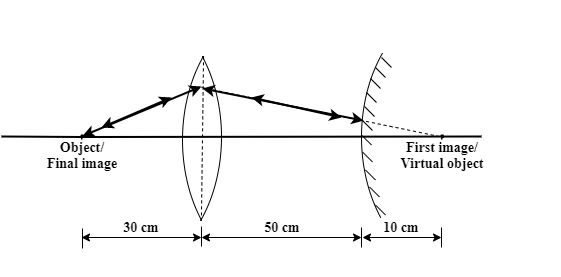
To produce an upright image exactly at the place of the object the light rays must come back through the same path it has traveled. So, you need to place the convex mirror in a position such that at each point on the mirror the ray becomes perpendicular to the surface. That can happen only if the object (virtual) is at the center of curvature of the convex mirror.

Formula used:
Lens formula:
$\dfrac{1}{v} = \dfrac{1}{u} + \dfrac{1}{f}$ …….(1)
Where,
$f$ is the focal length of the lens,
$v$ is the image distance from the lens,
$u$ is the object distance from the lens.
Mirror formula:
$\dfrac{1}{{u'}} + \dfrac{1}{{v'}} = \dfrac{1}{{f'}}$ …...(2)
Where,
$f’$ is the focal length of the mirror,
$v’$ is the image distance from the mirror,
$u’$ is the object distance from the mirror.

Complete step by step solution:
Given:
The object is at 30 cm distance from the lens, i.e. $u = - 30cm$.
Focal length of the convex lens is 20 cm, i.e. $f = 20cm$.
Radius of curvature(R) for the convex mirror is 10cm, i.e. $R = 2f' = 10cm$.
The final image formed by the lens must be at the place of the original object.
To find the Position where the convex mirror must be placed.

Step 1
Substitute the values of u and f in eq.(1) to find $v$ as:

$$\dfrac{1}{v} = \dfrac{1}{{ - 30}} + \dfrac{1}{{20}} \\\ \Rightarrow \dfrac{1}{v} = \dfrac{{3 - 2}}{{60}} \\\ \Rightarrow v = 60cm \\\$$

So, the image is supposed to produce on the opposite side at a distance of 60 cm.

Step 2
Now, try to find an argument of how the mirror should function so that the final image is produced at the place of the object. Since the path of the light ray is always reversible, so we can argue that if we replace the image(produced by the lens) by the object then the new image will be formed at the place of the original object. And exactly this has to be done by the convex mirror. You need to place the mirror in such a way that the position of the object(w.r.t the mirror) and image(w.r.t the mirror) coincides.

Step 3
Try to find where the position of the object(w.r.t the mirror) must be such that the image also forms at the same place.
Let us assume $u' = v' = x$. Now, substitute it in eq.(2) to get,
$\dfrac{1}{x} + \dfrac{1}{x} = \dfrac{1}{{f'}} \\\ \Rightarrow \dfrac{2}{x} = \dfrac{1}{{f'}} \\\ \Rightarrow x = 2f' = R = 10cm \\\$

Step 4
Hence, the object(virtual) w.r.t the mirror which is the first image formed by the lens must be at 10 cm right of the mirror. So, the position of the mirror must be 10 cm before the first image is formed, i.e. at $(60 - 10)cm = 50cm$from the lens.

$\therefore$ The convex mirror must be placed at (c) 50 cm distance from the lens. Hence option (C) is the correct answer.

Note:
Many students might get confused by the complexity of the arguments here. But just follow the path of light rays and its reversible property. Also, don’t get confused by the concept of a virtual object and the virtual image. If some converging beam reflects before actually meeting then for the mirror the object is not real it’s virtual and similarly after reflection if the rays diverge then the image is virtual.