Question

A loop is formed by two parallel conductors connected by a pure inductor with inductance $L = 0.1$ H an conducting rod of mass $m = 0.1$ kg which can slide freely without friction over the conductors. The conductors located in a horizontal plane in a uniform vertical magnetic field $B = 2.0$ T. The distance between the conduct is 1.0 m. At the instant $t = 0$, the rod is given velocity 4 m/s directed to the right. If the resistance of the loop negligible, find the amplitude of oscillation of the rod in cm.

Answer 1

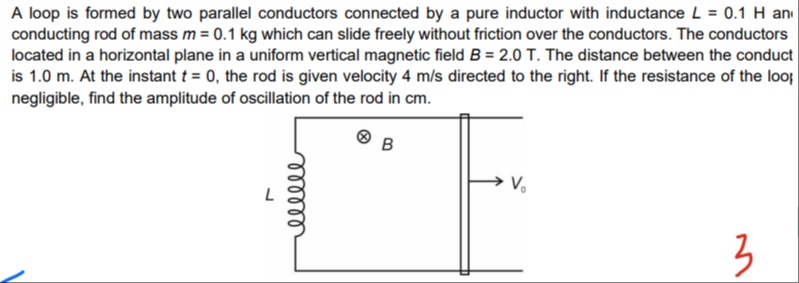
20

Answer 2

The system consists of a conducting rod of mass $m$ sliding on two parallel conductors connected by an inductor of inductance $L$. The system is in a uniform vertical magnetic field $B$. The distance between the conductors is $d$. The resistance of the loop is negligible.

Let $x$ be the position of the rod from a reference point. The area of the loop is $A = dx$. The magnetic flux through the loop is $\Phi = BA = Bdx$. When the rod moves with velocity $v = \frac{dx}{dt}$, an electromotive force (EMF) is induced in the loop: $\mathcal{E} = -\frac{d\Phi}{dt} = -\frac{d}{dt}(Bdx) = -Bd\frac{dx}{dt} = -Bdv$.

By Lenz's law, the induced current will flow in a direction that opposes the change in magnetic flux. If the rod moves to the right (increasing $x$), the flux into the page increases. The induced current will create a magnetic field out of the page, so the current flows counterclockwise. The loop consists of the induced EMF and the inductor. Since the resistance is negligible, the voltage across the inductor must balance the induced EMF: $L\frac{di}{dt} = -\mathcal{E} = -(-Bdv) = Bdv$. (1)

The magnetic force on the rod is given by $\vec{F}_m = i(\vec{l} \times \vec{B})$. The length vector $\vec{l}$ is in the direction of the current through the rod, which is downwards (if the current is counterclockwise as the rod moves to the right). The magnetic field $\vec{B}$ is into the page. The force is $\vec{F}_m = i(d\hat{j} \times B(-\hat{k})) = idB(-\hat{i})$. The force is to the left, opposing the motion. The magnitude of the magnetic force is $F_m = idB$. According to Newton's second law, the net force on the rod is $F_{net} = ma$. The only horizontal force is the magnetic force. $-F_m = m\frac{dv}{dt}$ $-idB = m\frac{dv}{dt}$. (2)

From equation (2), $i = -\frac{m}{dB}\frac{dv}{dt}$. Substitute this into equation (1): $L\frac{d}{dt}\left(-\frac{m}{dB}\frac{dv}{dt}\right) = Bdv$ $-\frac{mL}{dB}\frac{d^2v}{dt^2} = Bdv$ $\frac{d^2v}{dt^2} + \frac{B^2d^2}{mL}v = 0$.

This is the differential equation for the velocity $v(t)$. It is in the form of a simple harmonic oscillator equation $\frac{d^2v}{dt^2} + \omega^2 v = 0$, where the angular frequency of oscillation is $\omega = \sqrt{\frac{B^2d^2}{mL}}$.

Let's express the current $i$ in terms of displacement. From equation (1), integrating with respect to time gives $Li = \int Bdv dt = Bd\int v dt = Bd(x - x_0)$, where $x_0$ is the position where the current is zero. Let $x' = x - x_0$ be the displacement from the equilibrium position where the current is zero. Then $Li = Bdx'$, so $i = \frac{Bd}{L}x'$. Substitute this into equation (2): $-\left(\frac{Bd}{L}x'\right)dB = m\frac{d}{dt}\left(\frac{dx'}{dt}\right)$ $-\frac{B^2d^2}{L}x' = m\frac{d^2x'}{dt^2}$ $m\frac{d^2x'}{dt^2} + \frac{B^2d^2}{L}x' = 0$.

This is the differential equation for the displacement $x'(t)$. It is also the equation of SHM with the same angular frequency $\omega = \sqrt{\frac{B^2d^2}{mL}}$. The solution for the displacement is $x'(t) = A \cos(\omega t + \phi)$, where $A$ is the amplitude of oscillation.

We are given the values: $L = 0.1$ H, $m = 0.1$ kg, $B = 2.0$ T, $d = 1.0$ m. Calculate the angular frequency: $\omega = \sqrt{\frac{(2.0)^2 (1.0)^2}{(0.1)(0.1)}} = \sqrt{\frac{4 \times 1}{0.01}} = \sqrt{400} = 20$ rad/s.

We are given that at $t=0$, the rod is given velocity $v_0 = 4$ m/s directed to the right. We assume that before $t=0$, the system was at rest and there was no current. So, at $t=0$, the current is $i(0) = 0$. Since $i = \frac{Bd}{L}x'$, when $i(0) = 0$, we have $x'(0) = 0$. So, the initial position is the equilibrium position. At $t=0$, the initial conditions are $x'(0) = 0$ and $v(0) = 4$ m/s.

For SHM, the velocity is $v(t) = \frac{dx'}{dt} = -A\omega \sin(\omega t + \phi)$. At $t=0$, $x'(0) = A \cos(\phi) = 0$. This implies $\cos(\phi) = 0$, so $\phi = \pm \frac{\pi}{2}$. At $t=0$, $v(0) = -A\omega \sin(\phi) = 4$. If $\phi = \frac{\pi}{2}$, then $\sin(\phi) = 1$, so $-A\omega = 4$, which gives $A = -\frac{4}{\omega}$. Amplitude cannot be negative. If $\phi = -\frac{\pi}{2}$, then $\sin(\phi) = -1$, so $-A\omega (-1) = 4$, which gives $A\omega = 4$. The amplitude is $A = \frac{4}{\omega}$.

Substitute the value of $\omega$: $A = \frac{4}{20} = 0.2$ m.

The question asks for the amplitude in cm. $A = 0.2 \text{ m} = 0.2 \times 100 \text{ cm} = 20 \text{ cm}$.

Alternatively, we can use energy conservation. The total energy is the sum of kinetic energy and magnetic energy. $E = \frac{1}{2}mv^2 + \frac{1}{2}Li^2$. At $t=0$, $v(0) = 4$ m/s and $i(0) = 0$. $E_0 = \frac{1}{2}m v(0)^2 + \frac{1}{2}L i(0)^2 = \frac{1}{2}(0.1)(4)^2 + \frac{1}{2}(0.1)(0)^2 = \frac{1}{2}(0.1)(16) = 0.8$ J.

At the maximum displacement (amplitude $A$), the velocity is zero, and the current is maximum. Let $i_{max}$ be the maximum current. $E_{max} = \frac{1}{2}m v_{min}^2 + \frac{1}{2}L i_{max}^2 = \frac{1}{2}m (0)^2 + \frac{1}{2}L i_{max}^2 = \frac{1}{2}L i_{max}^2$. By energy conservation, $E_{max} = E_0$. $\frac{1}{2}L i_{max}^2 = 0.8$ $i_{max}^2 = \frac{2 \times 0.8}{L} = \frac{1.6}{0.1} = 16$. $i_{max} = \sqrt{16} = 4$ A.

The current is related to the displacement by $i = \frac{Bd}{L}x'$. The maximum current occurs at the maximum displacement (amplitude $A$). $i_{max} = \frac{Bd}{L}A$. $4 = \frac{(2.0)(1.0)}{0.1}A$ $4 = \frac{2}{0.1}A$ $4 = 20A$ $A = \frac{4}{20} = 0.2$ m.

Converting to cm: $A = 0.2 \times 100 = 20$ cm.