Question
Question: A loop carrying current I lies in the x-y plane as shown in the figure. The unit vector \[\widehat{k...
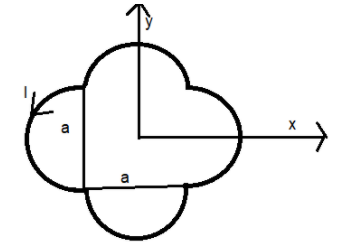
A loop carrying current I lies in the x-y plane as shown in the figure. The unit vector k is coming out of the plane of the paper. The magnetic moment of the current loop is?
Solution
The current carrying coil develops a magnetic field around the coil. The magnetic field is always perpendicular to the direction of current flow from the right-hand thumb rule. The area of the coil determines the magnetic field strength at a point.
Complete answer:
Let us consider the given coil as the source of the magnetic field. The magnetic moment is a quantity which determines the magnetic strength and its orientation with respect to the object that develops the magnetic field, here the coil. The magnetic moment is given by: μ=N(I×A), where N is the number of turns in the coil, I is the current through the coil and A is the area of the coil.
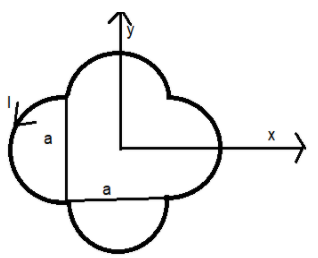
So, let us find the area of the given coil. It consists of four semicircles each of radius, r=2a and a square of side a.
i.e., The area of the coil is given by,
