Question
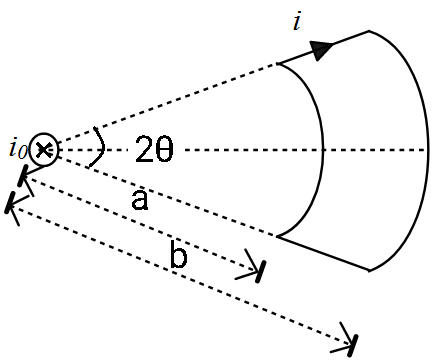
Question: A loop carrying a current i, lying in the plane of the paper, is in the field of long straight wire ...
A loop carrying a current i, lying in the plane of the paper, is in the field of long straight wire with current i0 (inward) as shown in figure. If the torque acting on the loop is given by τ=xπrμ0ii0[sinθ](b−a). Find x.
Solution
There is a wire carrying some current in the direction inside the plane of paper. The magnetic field created by this wire will have no effect on the circular regions of the loop as the magnetic field is tangential (parallel) to circular regions.
Formula used:
If a wire carries a current I, then the magnitude of magnetic field formed around it at a distance of r from it is:
B=2πrμ0I.
The force that a current carrying conductor experiences in a magnetic field is:
dF=idl×B
Complete answer:
Consider a small length dr on both the length segments carrying a current i. Since both of them along the radius of a circle, the magnetic field is perpendicular to both dr elements. Therefore the force on both of them is same and is equal to
dF=idr×B.
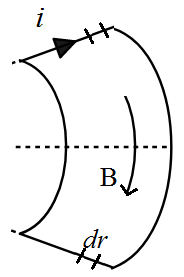
Here B is for the magnetic field produced by the wire carrying current i. Therefore around the wire we have magnetic field given by
B=2πrμ0i.
Substituting this value back in the force expression, we get:
dF=2πrμ0ii0dr.
Fleming's left hand rule will help in obtaining the direction of force on both the elements which are inwards and outwards for the two dr.
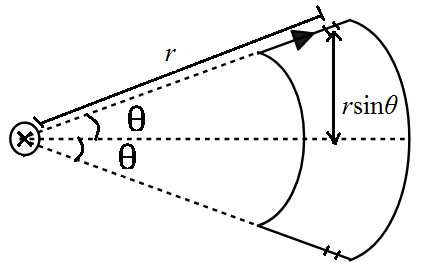
Let the distance of both the elements be r from the straight wire. This will give the distance of the upper and lower element to be rsinθ from the axis. So, the torque is
dτ=(2rsinθ)2πrμ0ii0dr.
Integrating from limits a to b will give us:
τ=πμ0ii0[sinθ]∫abdr
⟹τ=πμ0ii0[sinθ](b−a).
Therefore, in place of x, we must have 1/r so that our expression matches with the one in the question:
Note:
If we use Fleming's left hand rule we can find the direction of force in both the elements. In the upper element, the force is along the direction of i (perpendicular going inside the plane of paper) and as the current in the lower element is in the opposite direction so will be the force i.e., it is out from the plane of paper.
