Question

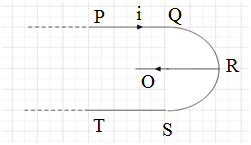
A long wire is bent into the shape PQRST as shown in the following Figure with QRS being a semicircle with centre O and radius r metre. A current I ampere flows through it in the direction$P\to Q\to R\to S\to T$. Then, the magnetic induction at the point O of the figure in a vacuum is

$A.\,{{\mu }_{0}}i\left[ \dfrac{1}{2\pi r}+\dfrac{1}{4r} \right]$
$B.\,{{\mu }_{0}}i\left[ \dfrac{1}{2\pi r}-\dfrac{1}{4r} \right]$
$C.\,\dfrac{\mu {}_{0}i}{4r}$
$D.\,\dfrac{\mu {}_{0}i}{\pi r}$

Answer 1

The reformed shape PQRST was earlier a wire, thus the magnetic field produced by the shape PQRST will be the same or equal to the amount of the magnetic field produced by the wire itself, thus usage of the formula for calculating the magnetic field produced by wire will be the correct option.

Formula used: $B=\dfrac{{{\mu }_{0}}I}{2\pi r}$

Complete step by step answer:
The magnetic field formula for a wire is,
$B=\dfrac{{{\mu }_{0}}I}{2\pi r}$
Where I is the flow of current and r is the radius/distance from the wire.
The magnetic field at $O$ due to the semi infinite segment PQ is equal to the half of the magnetic field due to an infinite wire.
The expression is given as follows:
${{B}_{PQ}}=\dfrac{1}{2}\dfrac{{{\mu }_{0}}i}{2\pi r}$
The magnetic field at $O$ due to the semi infinite segment ST is equal to the half of the magnetic field due to an infinite wire.
The expression is given as follows:
${{B}_{ST}}=\dfrac{1}{2}\dfrac{{{\mu }_{0}}i}{2\pi r}$
The magnetic field at $O$ due to the semi circle QRS is,
${{B}_{QRS}}=\dfrac{1}{2}\dfrac{{{\mu }_{0}}i}{4r}$

The total magnetic field at the point O is the sum of the magnetic fields produced at the semi infinite segment PQ, at the semi circle QRS and at the semi infinite segment ST.
Therefore, the total magnetic induction is,
${{B}_{total}}={{B}_{PQ}}+{{B}_{ST}}+{{B}_{QRS}}$
Substitute the obtained values in the above equation.
${{B}_{total}}=\dfrac{1}{2}\dfrac{{{\mu }_{0}}i}{2\pi r}+\dfrac{1}{2}\dfrac{{{\mu }_{0}}i}{2\pi r}+\dfrac{1}{2}\dfrac{{{\mu }_{0}}i}{4r}$
Upon further solving, we get,
${{B}_{total}}={{\mu }_{0}}i\left[ \dfrac{1}{2\pi r}+\dfrac{1}{4r} \right]$.
As the value the magnetic induction at the point O due to the magnetic field produced at the semi infinite segment PQ, at the semi circle QRS and at the semi infinite segment ST is ${{\mu }_{0}}i\left[ \dfrac{1}{2\pi r}+\dfrac{1}{4r} \right]$.

So, the correct answer is “Option A”.

Note: The things to be on your figure tips for further information on solving these types of problems are: There are different forms of the magnetic field formula. If the magnetic field produced is at some angle to the plane, then the formula to be used is, $B={}^{F}/{}_{IL\sin \theta }$.