Question
Question: A long uniform rod of length \( L \) , mass \( M \) is free to rotate in a horizontal plane about a ...
A long uniform rod of length L , mass M is free to rotate in a horizontal plane about a vertical axis through its end. Two springs of constant K each are connected as shown. On equilibrium, the road was horizontal. The frequency of small oscillation of rod if displaced slightly will be:
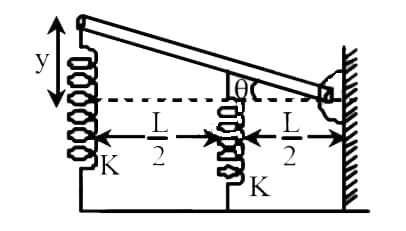
(A) 2π1M15K
(B) 2π14M15
(C) 2π14M3K
(D) 2π14M15K
Solution
If a spring is stretched or compressed, it is displaced from its original position. As a result, restoring force tends to retract the spring back to its equilibrium position. Restoring force of the spring is proportional to the displacement of the spring.
When the rod displaced slightly from its original position the connected spring stretched. Where restoring force of one spring F is proportional to its displacement y
∴F1∝y or, F1=Ky ( K is the spring constant)
And torque τ is proportional to the angular displacement θ
∴τ∝θ
⇒τ=Kθ
K is the torsion constant that is torque per unit angular displacement. If the moment of inertia of the body is I and the angular acceleration is α
Then, τ=−Iα .
Complete Step By Step Answer:
Let the uniform rod be displaced slightly at the angle of θ
Displacement of the spring be y and y1
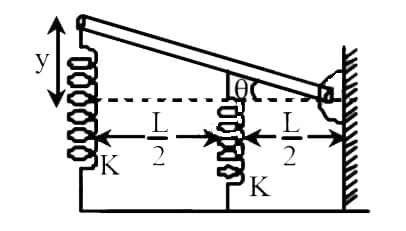
As the image is given we can calculate the value of θ is, θ=Ly
Also, θ=2Ly1
∴ y=Lθ and y1=2Lθ
Now let the force applied on the two rods are F1 and F2
Hence the spring constant is K
F1=Ky =KLθ
F2=Ky1 =2KLθ
The restoring Torque due to the elastic force of the spring is:
τ=(F1cosθ2L×F2cosθL)
⇒τ=(2F1+F2)cosθ
Here θ is very small, hence we can assume cosθ≃1
∴τ=(4KLθ+KLθ)L
=(4Kθ+Kθ)L2
=(45KLθ)L2
Now, Net Torque τ=(45KLθ)L2 =−Iα ( α= angular acceleration)
⇒(45KLθ)L2=(3ML2)α ( ∵I=−(3ML2) )
⇒α=−4m15Kθ
As we know α=−ω2θ
Putting the value we get, ω2=4m15K
∵ω=2πf=4m15K
Hence, the value of frequency f=2π14m15K
∴ A correct answer is an option (D).
Note:
If a spring is attached to a hook and the other is attached to an object with mass and hangs down vertically. The object will have two forces. One is restoring the force of the spring directly upward. The other will be the force of gravity acting on the mass directly downward. When the mass is not moving the net force is zero.
