Question

A long thread is wrapped around a reel. If one end of the thread is held in hand and the reel is allowed to fall under gravity, then the acceleration of the reel will be:
(A) $g$
(B) $\dfrac{2}{3}g$
(C) $\dfrac{3}{2}g$
(D) Zero

Answer 1

Hint : The forces acting on the reel are the weight of the body and the Torque on the thread. There is a net torque on the body due to the different line of action of the weight and the tension. So from the equation of motion we can find the acceleration.

Formula used: In this solution we will be using the following formula;
$\Rightarrow {\vec F_{NET}} = m\vec a$ where ${F_{NET}}$ is the net force on a body, $m$ is the mass and $a$ is the linear acceleration of the body.
$\Rightarrow {\tau _{NET}} = I\alpha$ where ${\tau _{NET}}$ is the net torque on a body, $I$ is the moment of inertia of the body and $\alpha$ is the angular acceleration.
$\Rightarrow I = \dfrac{1}{2}m{R^2}$ where $I$ is the moment of inertia of a disc or solid cylinder, and $R$ is the radius of the cylinder.
$\Rightarrow a = \alpha R$ where $a,\alpha ,R$ are already defined above.

Complete step by step answer

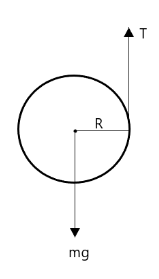
From the diagram above, the tension in the string is acting on the surface of the reel while the weight is acting at the centre of the reel. Hence, besides the forces themselves being analysed, the torque generated due to the difference in the line of action of the forces must also be analysed.
Firstly analysing the net force, we have
$\Rightarrow {F_{NET}} = T - mg = - ma$ (assuming up to be positive), thus
$\Rightarrow T - mg = - ma$
Now analysing the torque about the centre (or moment of a force as often called), we have
$\Rightarrow {\tau _{NET}} = I\alpha$
$\Rightarrow TR = I\alpha$
Where $I$ is the moment of inertia of a disc or solid cylinder, and $R$ is the radius of the cylinder, and $m$ is mass.
Hence from $a = \alpha R$ we have
$\Rightarrow \alpha = \dfrac{a}{R}$ ,
Also, the moment of inertia of a reel (cylinder) is given as
$\Rightarrow I = \dfrac{1}{2}m{R^2}$
Thus, by substitution,
$\Rightarrow TR = \dfrac{1}{2}m{R^2}\dfrac{a}{R}$
$\Rightarrow T = \dfrac{1}{2}ma$
Now inserting into $T - mg = - ma$ , we have
$\Rightarrow \dfrac{1}{2}ma - mg = - ma$
$\Rightarrow \dfrac{1}{2}ma + ma = mg$
By Addition, we get
$\Rightarrow \dfrac{3}{2}ma = mg$
Making $a$ subject of the formula
$\Rightarrow a = \dfrac{2}{3}g$
Hence, the correct option is B.

Note
Alternatively, it can be proven that $a = \dfrac{g}{{1 + \dfrac{I}{{m{R^2}}}}}$ , hence inserting the value of $I$ we get
$\Rightarrow a = \dfrac{g}{{1 + \dfrac{{\dfrac{1}{2}m{R^2}}}{{m{R^2}}}}}$
$\Rightarrow a = \dfrac{g}{{1 + \dfrac{1}{2}}} = \dfrac{g}{{\dfrac{3}{2}}} = \dfrac{2}{3}g$
Thus, $a = \dfrac{2}{3}g$.