Solveeit Logo
Login

Question

Question: A long thin walled pipe of radius R carries a current I along its length. The current density is uni...

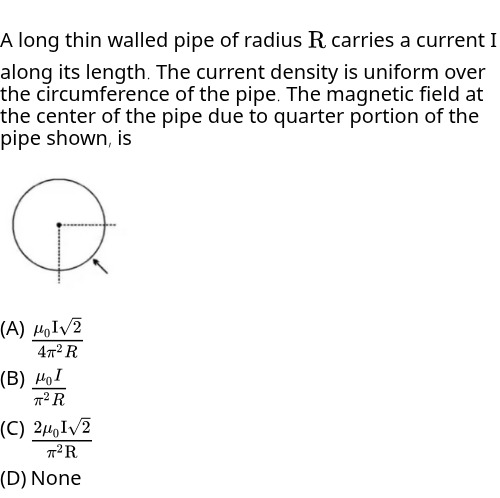
A long thin walled pipe of radius R carries a current I along its length. The current density is uniform over the circumference of the pipe. The magnetic field at the center of the pipe due to quarter portion of the pipe shown, is

A

μ0I24π2R\frac{\mu_0 I \sqrt{2}}{4\pi^2 R}

B

μ0Iπ2R\frac{\mu_0 I}{\pi^2 R}

C

2μ0I2π2R\frac{2\mu_0 I \sqrt{2}}{\pi^2 R}

D

None

Answer

(A)

Explanation

Solution

The current I flows axially along the pipe. The current density is uniform.

Consider a small element of the pipe of angular width dθd\theta. The current through this element is dI=(I/2π)dθdI = (I/2\pi) d\theta. This element acts as a long straight wire.

The magnetic field dBdB at the center of the pipe due to this element is dB=μ0dI2πR=μ0I4π2RdθdB = \frac{\mu_0 dI}{2\pi R} = \frac{\mu_0 I}{4\pi^2 R} d\theta.

If the current flows along the z-axis, and an element is at (Rcos⁡θ,Rsin⁡θ)(R\cos\theta, R\sin\theta), the magnetic field dB⃗d\vec{B} at the origin is tangential to a circle of radius R, having components dBx=−dBsin⁡θdB_x = -dB \sin\theta and dBy=dBcos⁡θdB_y = dB \cos\theta.

For a quarter portion (e.g., from θ=−π/2\theta = -\pi/2 to 00 as per the figure):

Bx=∫−π/20−μ0I4π2Rsin⁡θdθ=μ0I4π2RB_x = \int_{-\pi/2}^{0} -\frac{\mu_0 I}{4\pi^2 R} \sin\theta d\theta = \frac{\mu_0 I}{4\pi^2 R}

By=∫−π/20μ0I4π2Rcos⁡θdθ=μ0I4π2RB_y = \int_{-\pi/2}^{0} \frac{\mu_0 I}{4\pi^2 R} \cos\theta d\theta = \frac{\mu_0 I}{4\pi^2 R}

The magnitude of the resultant field is B=Bx2+By2=2(μ0I4π2R)2=μ0I24π2RB = \sqrt{B_x^2 + B_y^2} = \sqrt{2 \left(\frac{\mu_0 I}{4\pi^2 R}\right)^2} = \frac{\mu_0 I \sqrt{2}}{4\pi^2 R}.