Question

A long thin tube has two different cross sections and liquid flows inside it. Take two points A and B at the same horizontal level. Cross section A is larger than B then,

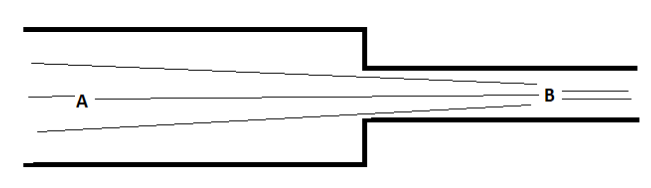
A. ${P_A} > {P_B}$
B. ${P_B} > {P_A}$
C. ${P_A} = {P_B}$
D. ${V_B} > {V_A}$

Answer 1

As the liquids are incompressible, the rate of flow into an area must equal the rate of flow out of an area. This is known as the equation of continuity. The equation of continuity can show how much the speed of a liquid increases when it flows through a smaller area.

Formula used:
The equation of continuity ${A_A}{V_A} = {A_B}{V_B}$ is used where ${A_A}$ is the area of cross section at point $A$, ${A_B}$ is the area of cross section at point $B$, ${V_A}$ is the velocity of fluid at point $A$and ${V_B}$ is the velocity of fluid at point $B$.
The Bernoulli’s equation $P + \dfrac{1}{2}\rho {v^2} + \rho gh = C$ is used where $P$is the pressure, $\rho$is the density, $v$is the velocity, $g$is the acceleration due to gravity and $h$is the height.

Complete answer:
Let there be two cross sections at points $A$ and $B$ of different areas, ${A_A}$ and ${A_B}$ respectively. Let the velocities at these points be ${V_A}$ and ${V_B}$ respectively. Since the fluid is incompressible, the volume that flows through any point of the pipe in a given time is constant. This is called the “continuity equation”.
${A_A}{V_A} = {A_B}{V_B}$ . That is, when the area is smaller, the velocity is bigger. That is ${V_B} > {V_A}$.
$\therefore$ Option (D) is correct.
Bernoulli's principle tells us how pressure and velocity are inversely proportional. In this case, where a fluid flows into a narrower cross section, the pressure decreases as the velocity increases. As a matter of fact, it is the difference in pressure that sustains the motion towards the smaller cross section.
Bernoulli’s equation is
$P + \dfrac{1}{2}\rho {v^2} + \rho gh = C$, where $C$ is a constant.
The term $\rho gh$ is derived from the gravitational potential energy. Consider two points that are at the same height. It is clear from the above that, the more the velocity, the lesser the pressure. That is, ${P_A} > {P_B}$.
$\therefore$ Option (A) is correct.

So, the correct answers are “Option A and D”.

Note:
Candidates can get confused when they use the formula $P = \dfrac{F}{A}$ as it says pressure and area are inversely proportional. The pressure and area are inversely proportional to each other i.e., when area decreases pressure exerted on that area increases. When area increases pressure exerted on that area decreases.