Question

A long string with a charge of $\lambda$ per unit length passes through an imaginary cube of edge length a. The maximum flux of the electric field through the cube will be:
A. $\lambda a/ \epsilon_0$
B. $\sqrt{2} \lambda a/ \epsilon_0$
C. $6 \lambda a^2/ \epsilon_0$
D. $\sqrt{3} \lambda a/ \epsilon_0$

Answer 1

There is a direct expression to find flux through a body and is called Gauss’s law. Flux is nothing but the density of field lines crossing a unit area. Amount of flux will be decided by the amount of charge present in the cube.

Formula used:
Charge can be obtained from charge density as:
$q=\lambda l$
Gauss’s law:
"The flux through any surface enclosing charge q is $q/ \epsilon_0$ or
$\phi = \dfrac{ q}{ \epsilon_0}$

Complete step by step answer:
We are given a long string with line charge density $\lambda$ therefore, the charge obtained when this string passes through the cube (parallel to its base), we see that the total charge we will get will be:
$q= \lambda a$
Consider the figure:

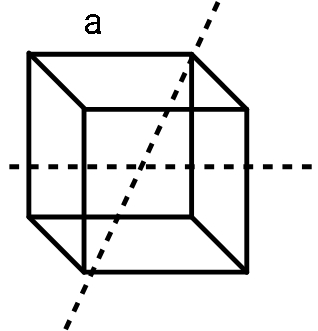
To get maximum flux outside the box, the maximum length of this string should pass through the box. So, we choose a cross diagonal orientation of such a string. The total length of the string in the box will be given as:
$l= \sqrt{2a^2 + a^2}$
This expression comes as a result of Pythagoras theorem applied to the triangle with our body diagonal as its hypotenuse l, base diagonal $\sqrt{2} a$ as its base and one side a as its perpendicular.
This gives us total length as:
$l= \sqrt{3} a$
So, the charge becomes
$q= \lambda \sqrt{3} a$
Keeping this in Gauss’s law, we get required maximum flux as:
$\phi = \dfrac{ \lambda \sqrt{3} a}{ \epsilon_0}$

Therefore the correct answer is option (D). $\sqrt{3} \lambda a/ \epsilon_0$.

Note:
From the question, the word maximum is quite important. One might naively conclude the wrong answer if the placement of the string in the box is wrong. The base diagonal $\sqrt{2} a$ is nothing but the diagonal length in a square, as the base of a cube is just a square.