Question

A long straight wire carries a current of 35A. What is the magnitude of the field B at a point 20cm from the wire?

Answer 1

Hint: We will start by stating some general result and we will start by understanding what a magnetic field is. Then we will assume the angles in the figure and apply the formula for the magnetic field due to a conductor. Refer to the solution below.

Formula used: $\dfrac{{{\mu _0}I}}{{4\pi r}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right)$, ${B_P} = \dfrac{{{\mu _0}I}}{{2\pi r}}$.

Complete step-by-step solution -
Magnetic field is typically used as an area in which magnetism operates. This magnetism force is usually created by moving charge or other magnetic substance.
The value of current as per given in the question is- $I = 35A$
The value of distance as per given in the question is- $r = 20cm = 0.2m$
We will state a general result over here. Let’s assume a current carrying conductor (refer to the figure below).

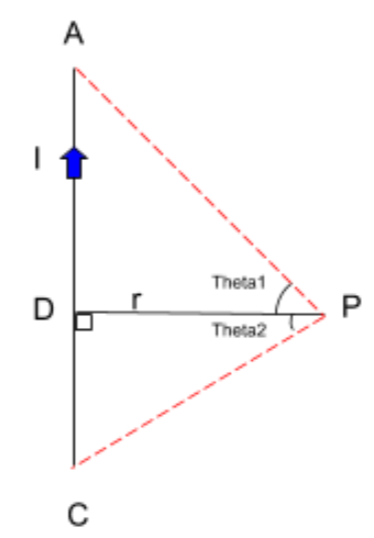
Let's assume that the angle $\angle APD$ is ${\theta _1}$ and the angle $\angle DPC$ is ${\theta _2}$.
Now, the magnetic field at any point due to the finite conductor will always be-
$\Rightarrow \dfrac{{{\mu _0}I}}{{4\pi r}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right)$
As we know for an infinite conductor-
$\Rightarrow {\theta _1} = {\theta _2} = 90^\circ$
The magnetic field at point P due to the finite conductor will be-
$\Rightarrow {B_P} = \dfrac{{{\mu _0}I}}{{2\pi r}}$
We know that the value of ${\mu _0}$ is $4\pi \times {10^{ - 7}}$. Substituting this value along with the other values in the above equation-
$\Rightarrow {B_P} = \dfrac{{{\mu _0}I}}{{2\pi r}} \\\ \\\ \Rightarrow {B_P} = \dfrac{{4\pi \times {{10}^{ - 7}} \times 35}}{{2\pi \times 0.2}} \\\ \\\ \Rightarrow {B_P} = \dfrac{{2 \times {{10}^{ - 6}} \times 35}}{2} \\\ \\\ \Rightarrow {B_P} = 35 \times {10^{ - 6}}T \\\$

Note: The actual rate of flow of charge is generally defined. We now know that fixed charges produce an electric field commensurate with the scale of the charge. It's the same theory that traveling charges generate magnetic fields equal to the current, which creates a magnetic influence on the existing current carrying conductor surrounding them. For example, passage of electrons on the nuclear orbits, this magnetic field is usually due to the subatomic particles in the conductor.