Question

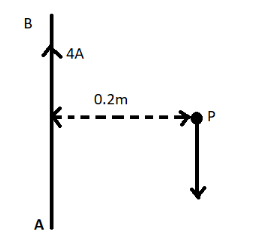
A long straight wire $AB$ carries a current of $4\,A$. A proton $P$ travels at $4 \times {10^6}\,m/s$ parallel to the wire $0.2\,m$ from it and in a direction opposite to the current as shown in the figure. Calculate the force which the magnetic field due to the current carrying wire exerts on the proton. Also specify its direction.

Answer 1

In order to answer this problem let us first understand about the Fleming left hand rule. When a current-carrying conductor is exposed to an external magnetic field, it is subjected to a force that is perpendicular to both the field and the current flow direction. John Ambrose Fleming was the one who came up with the idea.

Formula used:
$F = qvB\sin \theta$
Where, $F =$ magnetic force, $q =$Charge of moving particle, $v =$Particle velocity, $B =$Magnetic field and $\theta =$Angle between velocity and magnetic field vectors.
$B = \dfrac{{{\mu _o}I}}{{2\pi r}}$
Where $\;I$ is the current, $r$ is the shortest distance to the cable, and ${\mu _o}$ is the permeability of free space for a long straight wire.

Complete step by step answer:
Let us get some idea about the magnetic force. Because of their motion, magnetic force causes attraction or repulsion between electrically charged particles. It is the fundamental force that causes effects like the operation of electric motors and the attraction of magnets to iron. It is given by:
$F = qvB\sin \theta$..................[$equation - 1$]
The magnetic field is the region surrounding a magnet where a magnetic force is felt.
$B = \dfrac{{{\mu _o}I}}{{2\pi r}}$..............[$equation - 2$]
Now let’s solve the problem: Taking the value of B from $equation - 2$ and putting it into $equation - 1$ we get
$F = \dfrac{{{\mu _o}I}}{{2\pi }}\dfrac{I}{r}qv\sin \theta$
Given:
$v = 4 \times {10^6}m/s$
$\Rightarrow q = 1.6 \times {10^{ - 19}}C$
$\Rightarrow I = 4\,A$
$\Rightarrow r = 0.2\,m$
$\Rightarrow F = \dfrac{{2 \times {{10}^{ - 7}} \times 4 \times 1.6 \times {{10}^{ - 19}} \times 4 \times {{10}^6} \times \sin {{90}^ \circ }}}{{0.2}}$
$\Rightarrow F = \dfrac{{32 \times 1.6 \times {{10}^{ - 20}}}}{{0.2}}$
$\therefore F = 2.56 \times {10^{ - 18}}\,N$

Hence, the force which the magnetic field due to the current carrying wire exerts on the proton is $2.56 \times {10^{ - 18}}\,N$ and it acts in the plane of paper away from the wire.

Note: So we saw that to solve this kind of problem we should have knowledge about the magnetic field , magnetic force as well as Fleming left hand rule. A long straight wire's magnetic field has more consequences than one would think. Each current segment generates a magnetic field similar to that of a long straight wire, and the total field of any form current is equal to the vector sum of the fields produced by each segment.