Question

A long straight solid conductor of radius $8cm$ carries a current of $2A$, which is uniformly distributed over its circular cross-section. Find the magnetic field induction at a distance of $3cm$ from the axis of the conductor.

Answer 1

The problem is based on the concept of the uniform current density and the ampere circuital law. The ampere circuital law state that $\oint {\overrightarrow B } .\overrightarrow {dl} = {\mu _0}{I_{enclosed}}$ where, $\overrightarrow B =$ magnetic field, $\overrightarrow {dl} =$the elementary length, ${\mu _0} =$permeability of free space, ${I_{enclosed}} =$ current enclosed by the closed loop.

Complete step by step solution:
Step 1:

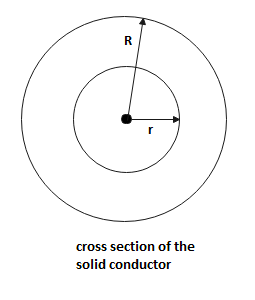
Here, $R = 8cm$or $R = 0.08m$and $r = 3cm$or $r = 0.03m$

Now the current $I$ is uniformly distributed along the cross section of the solid conductor. Therefore the current density,

$\Rightarrow j = \dfrac{I}{{\pi {R^2}}}$.

According to the question the total current,

$\Rightarrow I = 2A$.

Step 2: Now we have to calculate the magnetic field vector at a distance $rcm$from the centre. Therefore the total current enclosed by the loop of $rcm$ is${I_{enclosed}} = j\pi {r^2}$

$\Rightarrow {I_{enclosed}} = \dfrac{I}{{\pi {R^2}}} \times \pi {r^2}$
$\Rightarrow {I_{enclosed}} = \dfrac{{I{r^2}}}{{{R^2}}}$

Step 3: Now from the ampere circuital law we get, $\oint {\overrightarrow B } .\overrightarrow {dl} = {\mu _0}{I_{enclosed}}$

$\Rightarrow B \times (2\pi r) = {\mu _0}{I_{enclosed}}$ ---------- (1)

Now, ${I_{enclosed}} = \dfrac{{I{r^2}}}{{{R^2}}}$

$\Rightarrow {I_{enclosed}} = \dfrac{{2 \times {{0.03}^2}}}{{{{0.08}^2}}}$ [Since$R = 0.08m$, $r = 0.03m$and $I = 2A$ ]
$\Rightarrow {I_{enclosed}} = \dfrac{{2 \times 9}}{{64}}$
$\Rightarrow {I_{enclosed}} = \dfrac{9}{{32}}$

Then from equation (1) we get,

$B \times (2\pi r) = {\mu _0}{I_{enclosed}}$
$\Rightarrow B \times (2\pi \times 0.03) = \left( {4\pi \times {{10}^{ - 7}}} \right) \times \dfrac{9}{{32}}$

[Since the value of the permeability in free space,${\mu _0} = 4\pi \times {10^{ - 7}}H{m^{ - 1}}$]

$\Rightarrow B = 1.875 \times {10^{ - 6}}T$

Therefore the magnetic field induction at a distance of $3cm$from the axis of the conductor is$1.875 \times {10^{ - 6}}T$.

Note: Students should remember the ampere circuital law that is$\oint {\overrightarrow B } .\overrightarrow {dl} = {\mu _0}{I_{enclosed}}$.

And there is another method to solve this problem by direct formula.

Another method: The magnetic field at a distance $r$ from the centre of the conductor inside it that is $r < R$, where $R =$radius of the conductor is $B = \dfrac{{{\mu _0}Ir}}{{2\pi {R^2}}}$ where, ${\mu _0} =$permeability of free space, $\overrightarrow B =$ magnetic field, $I =$ total current that uniformly distributed over the conductor’s circular cross-section.
Now, $I = 2A$, $R = 8cm$or $R = 0.08m$ and $r = 3cm$ or $r = 0.03m$, ${\mu _0} = 4\pi \times {10^{ - 7}}H{m^{ - 1}}$
Therefore, $B = \dfrac{{{\mu _0}Ir}}{{2\pi {R^2}}}$

$\Rightarrow B = \dfrac{{4\pi \times {{10}^{ - 7}} \times 2 \times 0.03}}{{2\pi \times {{0.08}^2}}}$
$\Rightarrow B = 1.875 \times {10^{ - 6}}T$

Therefore the magnetic field induction at a distance of $3cm$ from the axis of the conductor is $1.875 \times {10^{ - 6}}T$.