Question

A long straight metallic cylindrical conductor of radius R carries a current I, which is uniformly distributed over its circular cross section. Find the magnetic field at a point at distance r from the axis of the wire, when point lies (i) inside and (ii) outside

Answer 1

Whenever an electric current passes through a wire, it creates a magnetic field around it. To calculate the solution of the following question we will first find the magnetic field then apply the ampere’s circuital law.

Complete answer:
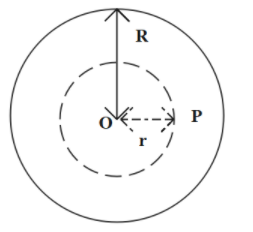
The figure below represents the section of solid metal wire of radius R, perpendicular to its length.
(i) Let the point P be lying inside the wire at a perpendicular distance r from the axis of the wire. Consider a circular path of radius r around the axis of the wire. By symmetry, the magnetic field produced due to current flowing in the wire at any point over this path is tangential to it and equal in magnitude at all points on this path.

Current enclosed by the closed path $= \dfrac{i}{{\pi {R^2}}} \times \pi {r^2} = \dfrac{{i{r^2}}}{{{R^2}}}$
Line integral of $\vec B$ over this closed path is
$\oint {\vec B.d\vec l = B2\pi r = {\mu _ \circ }{\mu _r}} \dfrac{{i{r^2}}}{{{R^2}}}$
Ampere’s circuital law is defined as the line integral of the magnetic field surrounding a closed loop is equal to the number of times the algebraic sum of currents passing through the loop.
Mathematically it can be written as, $\int {B.dl} = {\mu _ \circ }I$
Where ${\mu _ \circ }$ is the permeability of free space and $\int {B.dl}$ is the line integral of B around a closed path.
So, using Ampere’s circuital law
$\Rightarrow B = \dfrac{{\mu {}_ \circ {\mu _r}i{r^2}}}{{2\pi r{R^2}}} = \dfrac{{\mu {}_ \circ {\mu _r}ir}}{{2\pi r{R^2}}}$
(ii) When point P is outside the wire, $r > R$ so that the current enclosed by the closed path $i$
According to ampere’s circuital law,
\eqalign{ & \oint {\vec B.d\vec l = {\mu _ \circ }} i \cr & \Rightarrow B2\pi r = {\mu _ \circ }i \cr & \Rightarrow B = \dfrac{{{\mu _ \circ }i}}{{2\pi r}} \cr}
Hence, the magnetic field at a point at distance r from the axis of the wire, when point lies (i) inside is $\Rightarrow B = \dfrac{{\mu {}_ \circ {\mu _r}ir}}{{2\pi r{R^2}}}$ and (ii) outside is $B = \dfrac{{{\mu _ \circ }i}}{{2\pi r}}$

Note:
The region in which the magnetic field lines are at close distance to each other has a strong magnetic field and if the field lines are at far distance from each other, then the region has a weak magnetic force. Magnetic field lines do not intersect with each other. Magnetic field line is a vector quantity, it has both direction and magnitude.